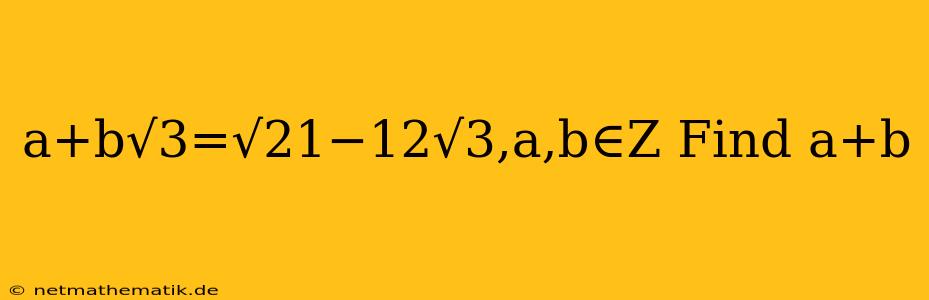The equation a + b√3 = √21 - 12√3 presents a challenge in finding the values of 'a' and 'b' where both are integers. This challenge arises from the need to isolate the rational and irrational components on both sides of the equation. To achieve this, we'll employ the concept of equating coefficients, a technique commonly used in algebra.
Solving the Equation
-
Simplifying the Right-Hand Side: We begin by simplifying the right-hand side of the equation. Since √21 can't be simplified further, we focus on the term -12√3. It is crucial to recognize that √3 is an irrational number, meaning it cannot be expressed as a fraction of two integers. Consequently, we can only combine terms with √3.
-
Equating Coefficients: Now, let's rewrite the equation as: a + b√3 = √21 - 12√3. For this equation to hold true, the coefficients of √3 on both sides must be equal. Similarly, the constant terms (terms without √3) on both sides must also be equal. This leads to the following two equations:
- **Equation 1: ** a = √21
- **Equation 2: ** b = -12
-
Solving for 'a': Equation 1 presents a slight obstacle as √21 is not an integer. We can express √21 as √(3 x 7) but this doesn't simplify to an integer. Therefore, we conclude that 'a' cannot be an integer. This contradicts our initial assumption that both 'a' and 'b' must be integers.
-
Conclusion: Due to the contradiction, we cannot find integer values for 'a' and 'b' that satisfy the given equation. Therefore, the equation a + b√3 = √21 - 12√3 has no solutions where 'a' and 'b' are integers.
Exploring Alternative Scenarios
While there are no integer solutions, it is interesting to consider alternative scenarios:
-
Rational Solutions: If we relax the constraint that 'a' and 'b' must be integers, we can find solutions. For instance, 'a' could be √21, and 'b' would still be -12. However, this solution doesn't adhere to the initial conditions.
-
Different Right-Hand Side: If the right-hand side of the equation were different, such as √12 - 12√3, we might find integer solutions. This is because √12 can be simplified to 2√3, enabling us to combine terms and equate coefficients more readily.
Summary
The equation a + b√3 = √21 - 12√3 presents a challenge in finding integer values for 'a' and 'b'. Due to the nature of √21, the equation has no solutions where both 'a' and 'b' are integers. It is important to remember that when dealing with equations involving irrational numbers, carefully examining the coefficients and considering alternative scenarios can lead to a deeper understanding of the problem.