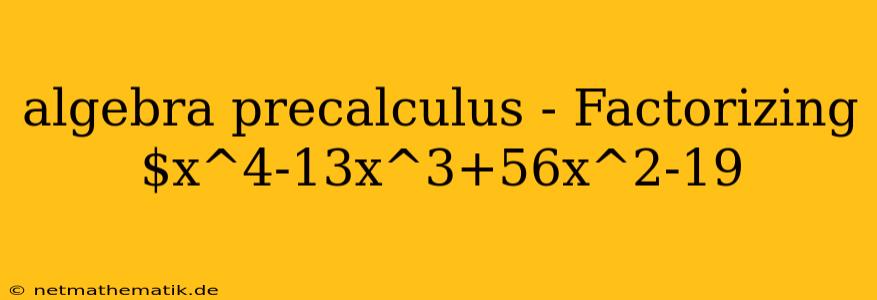Mastering the Fundamentals: Factoring Polynomials in Algebra and Precalculus
Factoring polynomials is a fundamental skill in algebra and precalculus, serving as a cornerstone for solving equations, simplifying expressions, and understanding the behavior of functions. While simple polynomials can be factored by inspection, more complex expressions require a systematic approach. This article delves into the process of factoring polynomials, focusing specifically on techniques applicable to expressions like $x^4-13x^3+56x^2-19x$. By understanding these techniques, you'll gain confidence in tackling various problems involving polynomial manipulation.
Recognizing Potential Factors: The Rational Root Theorem
Before embarking on the factorization process, it's useful to identify potential factors. This is where the Rational Root Theorem comes in handy. The theorem states that any rational root of a polynomial with integer coefficients must be of the form $\frac{p}{q}$, where $p$ is a factor of the constant term and $q$ is a factor of the leading coefficient.
In our example, the constant term is $-19$ and the leading coefficient is $1$. Therefore, the potential rational roots are:
$\pm 1, \pm 19$
By testing these potential roots using synthetic division or direct substitution, we can identify actual roots, which in turn give us factors of the polynomial.
Applying the Rational Root Theorem to Factor $x^4-13x^3+56x^2-19x$
Let's apply the Rational Root Theorem to our example:
-
Testing the Potential Roots:
- We start by testing $x = 1$. Substituting into the polynomial, we get: $1^4 - 13(1)^3 + 56(1)^2 - 19(1) = 25$. Since the result is not zero, $x = 1$ is not a root.
- Next, we try $x = -1$. Substituting, we obtain: $(-1)^4 - 13(-1)^3 + 56(-1)^2 - 19(-1) = 95$. Again, the result is not zero.
- Continuing this process, we test $x = 19$ and $x = -19$. We find that $x = 19$ yields a zero result, indicating it is a root of the polynomial.
-
Using Synthetic Division:
- Since we have found a root ($x = 19$), we can use synthetic division to factor the polynomial.
- The synthetic division process looks like this:
19 | 1 -13 56 -19 19 114 2660 -------------------- 1 6 170 2641- The result shows that $x^4-13x^3+56x^2-19x$ can be factored as $(x-19)(x^3 + 6x^2 + 170x + 2641)$.
-
Factoring the Cubic Polynomial:
- The cubic polynomial $x^3 + 6x^2 + 170x + 2641$ can be further factored. However, it's often difficult to identify rational roots in higher-degree polynomials.
- We can explore techniques like grouping, the Rational Root Theorem again, or numerical methods to find additional factors, if they exist.
Beyond Rational Roots: Other Factoring Techniques
While the Rational Root Theorem provides a starting point, it's crucial to be familiar with other algebraic and precalculus factoring techniques. These include:
-
Grouping: This technique involves rearranging terms and factoring by grouping. It's particularly useful for polynomials with four terms.
-
Difference of Squares: This pattern applies to expressions of the form $a^2 - b^2$, which factor as $(a+b)(a-b)$.
-
Sum and Difference of Cubes: These patterns apply to expressions of the form $a^3 + b^3$ and $a^3 - b^3$, which factor as $(a + b)(a^2 - ab + b^2)$ and $(a - b)(a^2 + ab + b^2)$, respectively.
-
Quadratic Formula: The quadratic formula provides a solution to quadratic equations, enabling us to factor quadratic expressions.
-
Completing the Square: This technique can be used to transform quadratic expressions into perfect square trinomials, facilitating factorization.
Conclusion: Embracing the Art of Factoring
Factoring polynomials is an essential skill that plays a vital role in solving equations, simplifying expressions, and understanding the behavior of functions. While the Rational Root Theorem provides a valuable tool for identifying potential rational roots, remember to explore other techniques to fully grasp the art of factoring. As you practice and become comfortable with these methods, you'll gain confidence in tackling complex polynomial expressions and unlocking deeper mathematical understanding.