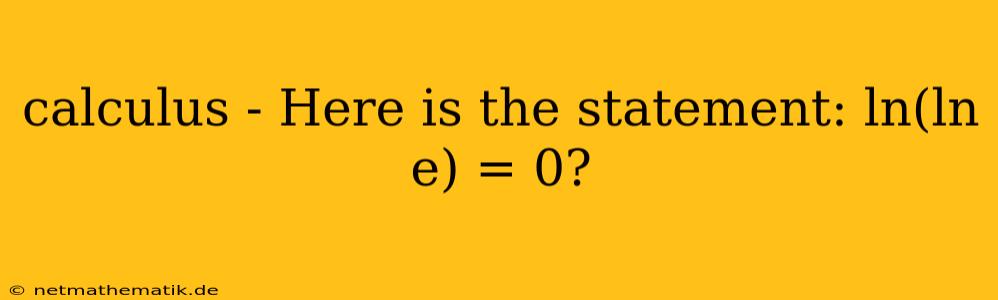The statement ln(ln e) = 0 is indeed true. Understanding this requires a grasp of the fundamental properties of logarithms and the special nature of the constant 'e'. Let's delve into the explanation.
Understanding Logarithms
Logarithms are the inverse operations of exponentiation. In simpler terms, if you have an equation like:
- b<sup>x</sup> = y
Then the logarithmic form of this equation would be:
- log<sub>b</sub>(y) = x
Here, b is the base of the logarithm. The most common bases are 10 (for the common logarithm, denoted as "log") and the mathematical constant 'e' (for the natural logarithm, denoted as "ln").
The Importance of 'e'
The constant 'e', approximately equal to 2.71828, is a fundamental mathematical constant that arises naturally in various fields like calculus, physics, and finance. It is the base of the natural logarithm. One of the key properties of 'e' is:
- ln(e) = 1
This follows directly from the definition of logarithms:
- If ln(e) = 1, then e<sup>1</sup> = e (which is true)
Evaluating ln(ln e)
Now, let's look at the expression ln(ln e).
- Inner Logarithm: We know that ln(e) = 1.
- Outer Logarithm: Therefore, we are left with ln(1).
Remembering that the logarithm of 1 to any base is always 0 (since any number raised to the power 0 equals 1), we can conclude:
- ln(1) = 0
Therefore, ln(ln e) = 0 is a true statement.
Calculus Applications of the Natural Logarithm
The natural logarithm, ln(x), has several important applications in calculus, particularly in differentiation and integration:
- Derivative: The derivative of ln(x) is simply 1/x.
- Integral: The integral of 1/x is ln(|x|) + C (where C is the constant of integration).
The natural logarithm also appears frequently in the solutions of differential equations and in modeling exponential growth and decay.
In Conclusion
The expression ln(ln e) = 0 is a true statement that illustrates the fundamental properties of logarithms and the special nature of the mathematical constant 'e'. This understanding is essential for further exploration of calculus and related fields where logarithms play a crucial role. The natural logarithm, in particular, is a powerful tool with diverse applications in various areas of mathematics and beyond.