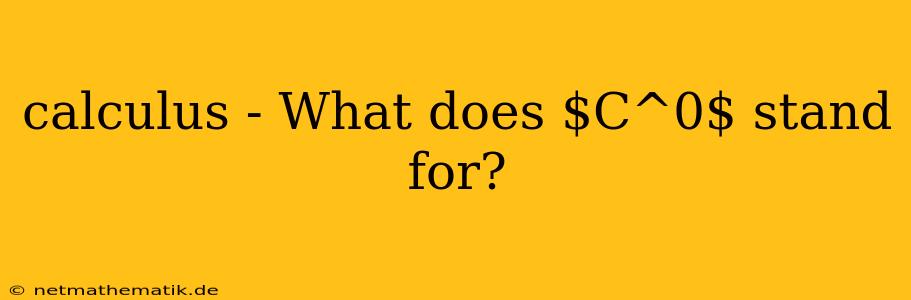In the realm of calculus, we often encounter the notation $C^0$, which might seem cryptic at first glance. This notation is a shorthand for describing a specific class of functions known as continuous functions. This article aims to demystify what $C^0$ represents and explore its significance within the context of calculus.
Understanding Continuity in Calculus
At its core, continuity refers to a function's ability to smoothly transition between points without any abrupt jumps or breaks. A continuous function is one where, as the input value changes infinitesimally, the output value also changes smoothly. This smooth variation is crucial in calculus, as it forms the foundation for many fundamental concepts like derivatives and integrals.
The Significance of $C^0$
The notation $C^0$ is used to denote the set of all continuous functions defined on a specific interval or domain. In essence, it's a classification system that groups together functions based on their continuity properties.
What Does the '0' Mean?
The superscript '0' in $C^0$ signifies that the functions in this set are continuous but not necessarily differentiable. In other words, we are only concerned with the continuity of the function itself, not the continuity of its derivative.
The Concept of Differentiability
A differentiable function is one where the derivative exists at every point in its domain. The derivative essentially measures the rate of change of a function. While continuity is a necessary condition for differentiability, it is not sufficient. A function can be continuous at a point but not differentiable at that point.
Examples of $C^0$ Functions
Here are some examples of functions that belong to the set $C^0$:
- Polynomial functions: All polynomial functions, such as $f(x) = x^2 + 3x - 2$, are continuous everywhere and therefore belong to $C^0$.
- Exponential functions: Functions like $f(x) = e^x$ are continuous for all real numbers.
- Trigonometric functions: Trigonometric functions like sine and cosine are continuous for all real numbers.
Examples of Functions Not in $C^0$
- Piecewise defined functions: Consider a function defined as follows:
This function has a discontinuity at x = 0, meaning it does not belong to $C^0$.f(x) = { x, if x < 0 x^2, if x >= 0 } - Functions with vertical asymptotes: Functions with vertical asymptotes, such as $f(x) = 1/x$, exhibit a break in continuity at the point where the asymptote occurs.
Importance of $C^0$ in Calculus
The concept of $C^0$ functions is fundamental to calculus because:
- Derivatives and Integrals: Many calculus operations, including differentiation and integration, rely on the concept of continuity. To find the derivative or integral of a function, the function must be continuous within the interval of interest.
- Solving Differential Equations: Differential equations are mathematical models that often involve functions and their derivatives. The concept of continuity plays a crucial role in finding solutions to these equations.
- Applications in Physics and Engineering: Continuity is a key concept in many areas of physics and engineering, including mechanics, thermodynamics, and fluid dynamics. For instance, when modeling physical systems, we often assume that certain quantities, such as velocity or temperature, are continuous.
The Hierarchy of Continuous Functions
While $C^0$ represents the set of all continuous functions, there are higher levels of continuity, denoted by $C^1$, $C^2$, and so on. These higher levels indicate the continuity of not only the function but also its derivatives.
- $C^1$ functions: Functions that are both continuous and have a continuous first derivative.
- $C^2$ functions: Functions that are continuous and have continuous first and second derivatives.
- $C^n$ functions: Functions that are continuous and have continuous derivatives up to the n-th order.
The hierarchy of continuous functions provides a more refined way to classify functions based on their smoothness and differentiability properties.
Conclusion
In the world of calculus, the notation $C^0$ serves as a succinct way to represent the class of continuous functions. Understanding the concept of continuity is essential for grasping many fundamental concepts in calculus, including derivatives, integrals, and differential equations. The $C^0$ notation provides a useful framework for classifying functions based on their continuity properties, paving the way for a deeper exploration of the nuances of mathematical analysis. Whether you're delving into advanced calculus concepts or simply studying the fundamentals, understanding the significance of $C^0$ functions is a valuable step towards mastering the beauty and power of this branch of mathematics.