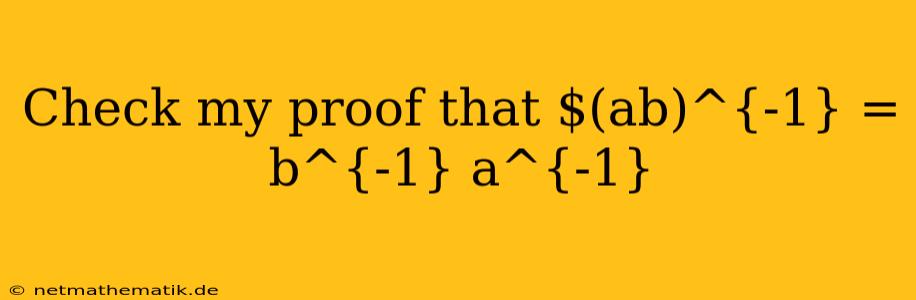In the realm of abstract algebra, particularly within the framework of group theory, understanding the inverse of a product is crucial. This concept, often referred to as the "reverse order law," states that the inverse of the product of two elements is equal to the product of their inverses in reverse order. Let's delve into a rigorous proof of this fundamental property and explore its implications.
Proving the Reverse Order Law
To formally demonstrate that $(ab)^{-1} = b^{-1}a^{-1}$, we'll employ the definition of an inverse element and the properties of group operations.
Recall: In a group, an element $a$ has a unique inverse, denoted as $a^{-1}$, such that:
$a * a^{-1} = a^{-1} * a = e$
where * represents the group operation and e is the identity element.
Proof:
-
Start with the product of the element and its inverse: $(ab) * (b^{-1}a^{-1})$.
-
Apply associativity of group operation: $a * (b * b^{-1}) * a^{-1}$
-
Utilize the inverse property: $a * e * a^{-1}$
-
Identity element property: $a * a^{-1}$
-
Again, apply the inverse property: $e$
Therefore, we have shown that:
$(ab) * (b^{-1}a^{-1}) = e$
-
Similarly, we can show that:
$(b^{-1}a^{-1}) * (ab) = e$
-
By definition, this implies that (b⁻¹a⁻¹) is the inverse of (ab), hence:
$(ab)^{-1} = b^{-1}a^{-1}$
Q.E.D.
Significance of the Result
This proof highlights a fundamental characteristic of group operations and has several important implications:
-
Inverse Order: The proof clarifies that the inverse of a product is found by taking the inverses of the factors in the reverse order. This is not merely a convention but a consequence of the group structure.
-
Matrix Inversion: The concept readily extends to matrix multiplication. For matrices A and B, (AB)⁻¹ = B⁻¹A⁻¹ holds true, provided both matrices are invertible. This property is essential for solving systems of linear equations and various matrix manipulations.
-
Polynomial Rings: The principle applies to polynomial rings where multiplication is defined as the product of polynomials. The inverse of a polynomial product follows the reverse order rule as well.
-
Abstract Algebra: The proof serves as a foundation for more complex algebraic structures. Its principle generalizes to rings, fields, and other algebraic systems, emphasizing the consistent nature of inverses within abstract algebra.
Understanding the Intuition
While the formal proof uses symbolic manipulation, the intuitive understanding of the reverse order law can be grasped as follows:
Imagine a sequence of actions, such as opening a door, turning on a light, and closing the door. To undo this sequence, you need to reverse the actions: close the light, turn off the light, and open the door. The inverse of the entire sequence is found by applying the inverses of each action in the reverse order.
Conclusion
The proof that $(ab)^{-1} = b^{-1}a^{-1}$ provides a foundational understanding of group structure and inverse operations. This property, often referred to as the reverse order law, is not just a mathematical curiosity but a fundamental principle that governs operations within various algebraic systems. It is essential for understanding the behavior of inverses within matrices, polynomials, and abstract algebra, simplifying complex operations and enabling the solution of various mathematical problems.