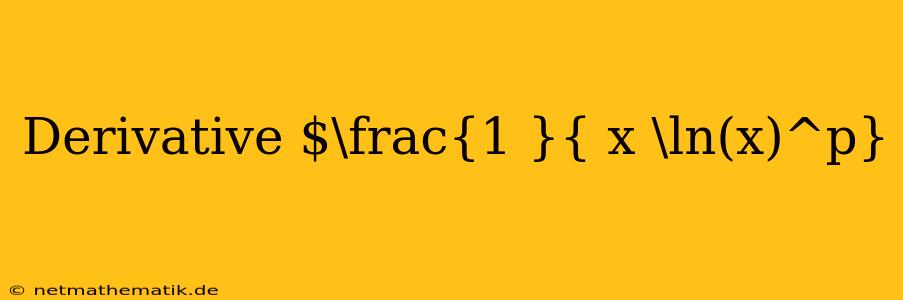Exploring the Derivative of 1/(x ln(x)^p)
The function $\frac{1}{x \ln(x)^p}$ represents a fascinating example of a function that combines logarithmic and power functions. Its derivative reveals a unique pattern and requires careful application of differentiation rules. This article delves into the process of finding the derivative of this function, exploring its properties, and highlighting its potential applications.
Understanding the Function
Before we embark on finding the derivative, let's analyze the function itself. It's essentially a product of two terms: $\frac{1}{x}$ and $\frac{1}{\ln(x)^p}$.
- 1/x: This term represents a simple reciprocal function, whose derivative is -1/x².
- 1/ln(x)^p: This term is a power function with a logarithmic base. The value of 'p' determines the behavior of the function. For instance, if 'p' is a positive integer, the function will approach infinity as 'x' approaches 1 from the right.
Calculating the Derivative
To find the derivative of $\frac{1}{x \ln(x)^p}$, we'll use the quotient rule. The quotient rule states that the derivative of a quotient of two functions, u(x) and v(x), is given by:
d/dx [u(x)/v(x)] = [v(x) * d/dx(u(x)) - u(x) * d/dx(v(x))] / [v(x)]²
In our case, u(x) = 1 and v(x) = x ln(x)^p.
-
Find the derivative of u(x): d/dx (1) = 0
-
Find the derivative of v(x): We'll need to apply the product rule and the chain rule here.
- d/dx [x ln(x)^p] = ln(x)^p + x * p * ln(x)^(p-1) * (1/x)
- Simplifying this, we get: d/dx [x ln(x)^p] = ln(x)^p + p * ln(x)^(p-1)
-
Apply the quotient rule: Substituting the values into the quotient rule:
d/dx [1 / (x ln(x)^p)] = [(x ln(x)^p) * 0 - 1 * (ln(x)^p + p * ln(x)^(p-1))] / [(x ln(x)^p)]² -
Simplify the result:
d/dx [1 / (x ln(x)^p)] = - (ln(x)^p + p * ln(x)^(p-1)) / (x ln(x)^p)²
Analyzing the Derivative
The derivative we obtained, - (ln(x)^p + p * ln(x)^(p-1)) / (x ln(x)^p)², is a complex function itself. It's important to analyze its key properties:
-
Domain: The function is defined for all x greater than 0, excluding x = 1. This is because ln(x) is only defined for positive values of x, and the function becomes undefined when x = 1 due to the denominator becoming zero.
-
Behavior:
- As x approaches 1 from the right, the derivative approaches negative infinity. This indicates that the original function has a vertical asymptote at x = 1.
- As x approaches infinity, the derivative approaches zero. This suggests that the original function approaches a horizontal asymptote as x increases without bound.
-
Impact of 'p':
- The value of 'p' significantly impacts the behavior of the derivative. For larger values of 'p', the term ln(x)^p will dominate the derivative, making it more negative for values of x close to 1.
Applications of the Derivative
The derivative of $\frac{1}{x \ln(x)^p}$ has applications in various fields:
-
Mathematical Analysis: It can be used to study the behavior of the original function, including its critical points, intervals of increase and decrease, and concavity.
-
Probability and Statistics: The function itself and its derivative can be used in probability density functions and related calculations.
-
Physics and Engineering: The derivative can be used in modeling and analysis of phenomena involving logarithmic growth or decay, such as radioactive decay or population growth.
Conclusion
The derivative of $\frac{1}{x \ln(x)^p}$ is a complex but fascinating result. It requires careful application of differentiation rules and highlights the interplay between logarithmic and power functions. Understanding its behavior and applications can provide valuable insights in various fields of mathematics, science, and engineering.