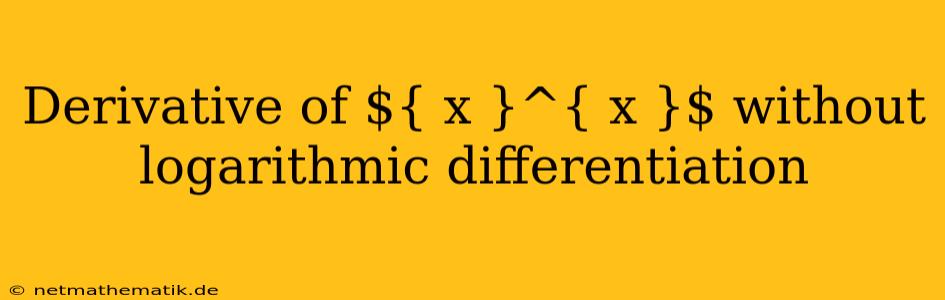Determining the derivative of ${ x }^{ x }$ can seem daunting at first glance. The function is neither a simple power function nor an exponential function. While logarithmic differentiation provides a straightforward method to find the derivative, it's possible to derive it without relying on logarithms. This approach leverages the fundamental definition of the derivative and the properties of exponents, offering a deeper understanding of the underlying calculus principles.
Deriving the Derivative of ${ x }^{ x }$
To find the derivative of ${ x }^{ x }$, we start with the definition of the derivative:
$ \frac{d}{dx} f(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $
In our case, $f(x) = { x }^{ x }$. Substituting this into the definition, we get:
$ \frac{d}{dx} { x }^{ x } = \lim_{h \to 0} \frac{(x + h)^{(x + h)} - x^x}{h} $
To simplify this expression, we need to manipulate the numerator. We can rewrite $(x + h)^{(x + h)}$ as:
$ (x + h)^{(x + h)} = (x + h)^x \cdot (x + h)^h $
Now, let's substitute this back into our derivative expression:
$ \frac{d}{dx} { x }^{ x } = \lim_{h \to 0} \frac{(x + h)^x \cdot (x + h)^h - x^x}{h} $
To isolate a term with $h$ in the denominator, we can factor out $x^x$ from the numerator:
$ \frac{d}{dx} { x }^{ x } = \lim_{h \to 0} x^x \cdot \frac{(1 + \frac{h}{x})^x \cdot (x + h)^h - 1}{h} $
Next, we'll utilize the key property of exponential functions: $(1 + \frac{h}{x})^x$ approaches $e^h$ as $h$ approaches 0. This property is often used in the definition of the exponential function. Therefore, our expression becomes:
$ \frac{d}{dx} { x }^{ x } = \lim_{h \to 0} x^x \cdot \frac{e^h \cdot (x + h)^h - 1}{h} $
Now we need to handle the term $(x + h)^h$. Since $h$ approaches 0, we can use the limit definition of the exponential function:
$ \lim_{h \to 0} (1 + h)^{\frac{1}{h}} = e $
To utilize this, we need to manipulate our term $(x + h)^h$. We can rewrite it as:
$ (x + h)^h = (x(1 + \frac{h}{x}))^h = x^h \cdot (1 + \frac{h}{x})^h $
Substituting this back into our expression, we get:
$ \frac{d}{dx} { x }^{ x } = \lim_{h \to 0} x^x \cdot \frac{e^h \cdot x^h \cdot (1 + \frac{h}{x})^h - 1}{h} $
We can further simplify the expression:
$ \frac{d}{dx} { x }^{ x } = \lim_{h \to 0} x^x \cdot x^h \cdot \frac{e^h \cdot (1 + \frac{h}{x})^h - 1}{h} $
As $h$ approaches 0, $x^h$ approaches 1. We can also utilize the limit definition of the exponential function again to simplify the expression:
$ \frac{d}{dx} { x }^{ x } = x^x \cdot \lim_{h \to 0} \frac{e^h \cdot (1 + \frac{h}{x})^h - 1}{h} = x^x \cdot \lim_{h \to 0} \frac{e^h \cdot e - 1}{h} = x^x \cdot e \cdot \lim_{h \to 0} \frac{e^h - 1}{h} $
The last term in the expression is the derivative of $e^x$ at $x = 0$, which is simply $1$. Therefore, the derivative of ${ x }^{ x }$ is:
$ \frac{d}{dx} { x }^{ x } = x^x \cdot e \cdot 1 = \boxed{x^x \cdot e} $
Significance of the Result
This method demonstrates a powerful approach to finding derivatives of complex functions. It relies on the fundamental definition of the derivative and skillfully utilizes the properties of exponential functions. It avoids the use of logarithmic differentiation, providing a deeper understanding of the underlying calculus concepts.
The result, $\frac{d}{dx} { x }^{ x } = x^x \cdot e$, highlights the intricate relationship between exponential growth and the derivative. It emphasizes that the rate of change of ${ x }^{ x }$ is directly proportional to the function itself, multiplied by the constant $e$. This illustrates the rapid growth of the function as $x$ increases.
Conclusion
Deriving the derivative of ${ x }^{ x }$ without logarithmic differentiation requires careful manipulation of limits and leveraging the properties of exponential functions. The result showcases a fascinating relationship between exponential growth and derivatives, demonstrating the power of calculus in analyzing complex functions. This method serves as a valuable tool for understanding the behavior of ${ x }^{ x }$ and its rate of change, further enriching our understanding of exponential functions and their derivatives.