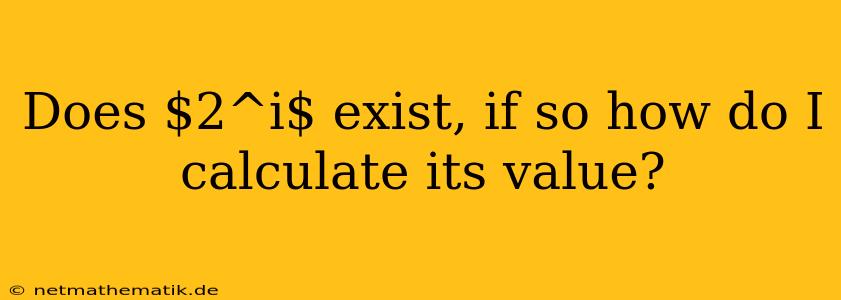The question of whether or not $2^i$ exists, where $i$ is the imaginary unit, might seem perplexing at first glance. After all, we are accustomed to exponents working with real numbers. However, the concept of exponentiation can be extended to complex numbers, including imaginary numbers, by leveraging the power of Euler's formula. This formula, a cornerstone of mathematics, provides a bridge between the world of complex exponentials and trigonometric functions, allowing us to understand and calculate the value of expressions like $2^i$.
Exploring Euler's Formula and its Application
Euler's formula is a remarkable mathematical identity that states:
$e^{i\theta} = cos(\theta) + i sin(\theta)$
where:
- e is Euler's number, the base of the natural logarithm, approximately equal to 2.71828
- i is the imaginary unit, defined as the square root of -1
- θ is an angle measured in radians
This formula establishes a profound connection between complex exponentials and trigonometric functions. The left side of the equation represents a complex exponential, while the right side expresses it in terms of cosine and sine functions.
Calculating $2^i$ using Euler's Formula
To calculate $2^i$, we can utilize the fact that any positive real number can be expressed as an exponential of $e$, the base of the natural logarithm. Therefore, we can rewrite $2^i$ as:
$2^i = (e^{ln(2)})^i = e^{i ln(2)}$
Now, we can apply Euler's formula to calculate $e^{i ln(2)}$:
$e^{i ln(2)} = cos(ln(2)) + i sin(ln(2))$
Therefore, the value of $2^i$ is a complex number with a real part of $cos(ln(2))$ and an imaginary part of $sin(ln(2))$.
Visualizing the Result
The result of $2^i$ is a complex number that can be represented graphically in the complex plane. The real part of the number corresponds to the horizontal axis, and the imaginary part corresponds to the vertical axis. The point representing $2^i$ lies at a distance of 1 from the origin, with an angle of $ln(2)$ radians with respect to the positive real axis.
Conclusion
The question of whether $2^i$ exists is answered with a resounding "yes!" By employing the powerful tool of Euler's formula, we can extend the concept of exponentiation to include complex numbers and calculate their values. While the result might seem abstract, it demonstrates the elegance and interconnectedness of mathematical concepts and their ability to bridge seemingly disparate areas of study.