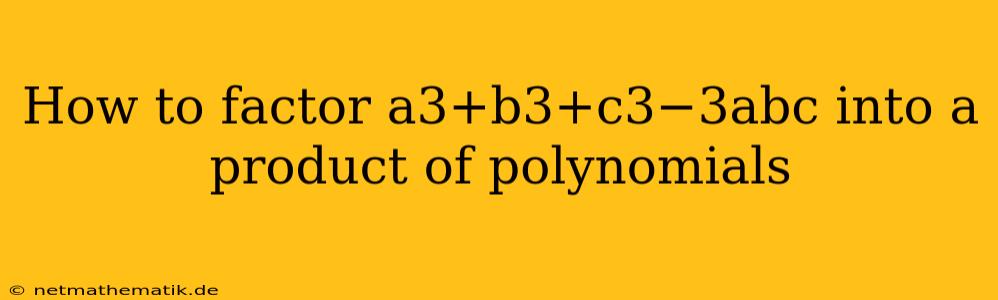Factoring expressions can be a powerful tool in algebra, allowing us to simplify complex expressions, solve equations, and gain a deeper understanding of mathematical relationships. One particularly intriguing factorization involves the expression a³ + b³ + c³ - 3abc. This expression, despite its seemingly complex structure, can be factored into a product of three linear polynomials. This factorization is not immediately obvious, but it holds significant implications in various fields, including geometry, number theory, and cryptography. Let's delve into the process of factoring a³ + b³ + c³ - 3abc and explore its applications.
The Factorization Process
The factorization of a³ + b³ + c³ - 3abc is based on a fundamental algebraic identity:
a³ + b³ + c³ - 3abc = (a + b + c)(a² + b² + c² - ab - ac - bc)
This identity can be derived through various methods, including direct multiplication of the right-hand side or using the concept of symmetric polynomials. To understand the derivation, we can start by expanding the right-hand side:
(a + b + c)(a² + b² + c² - ab - ac - bc) = a³ + ab² + ac² - a²b - a²c - abc + ba² + b³ + bc² - ab² - abc - b²c + ca² + cb² + c³ - abc - ac² - bc²
After simplifying, we notice that most terms cancel out, leaving us with:
a³ + b³ + c³ - 3abc
This verifies the factorization identity.
Understanding the Factorization
The factorization of a³ + b³ + c³ - 3abc reveals several interesting insights:
-
Symmetry: The expression and its factorization exhibit symmetry in the variables a, b, and c. This symmetry is reflected in the way the terms are arranged in the expression and the structure of the factors.
-
Roots: The factorization tells us that the expression becomes zero when a + b + c = 0. This is because the first factor (a + b + c) becomes zero, regardless of the values of the other factors.
-
Geometric Interpretation: The expression a³ + b³ + c³ - 3abc can be interpreted geometrically as the volume of a certain solid. This solid is known as the "tetrahedron", a three-dimensional shape with four triangular faces. The factorization allows us to express the volume of the tetrahedron in terms of the lengths of its edges.
Applications of the Factorization
The factorization of a³ + b³ + c³ - 3abc has numerous applications across various fields:
-
Solving Equations: The factorization can be used to solve cubic equations. For instance, if we encounter an equation of the form x³ + y³ + z³ - 3xyz = k, we can use the factorization to express the left-hand side as a product of linear factors. Setting the expression equal to k and solving for the factors can give us the solutions to the original equation.
-
Number Theory: The factorization has connections to number theory, specifically in the study of "sum of cubes" problems. The factorization can be used to explore relationships between cubes of integers and their sums.
-
Cryptography: The factorization has applications in cryptography, particularly in the development of "public-key cryptography" schemes. The difficulty of factoring large numbers into their prime factors forms the basis of many modern encryption algorithms.
-
Geometry: The factorization is used in various geometric problems, such as finding the volume of a tetrahedron. By expressing the volume in terms of the lengths of the edges, we can use the factorization to solve geometric problems involving tetrahedrons.
Examples of Using the Factorization
Let's look at a few examples illustrating the applications of the factorization:
Example 1: Solving a Cubic Equation
Consider the equation x³ + 8y³ - 27z³ - 18xyz = 0. Using the factorization, we can rewrite the left-hand side as:
(x + 2y - 3z)(x² + 4y² + 9z² - 2xy + 3xz - 6yz) = 0
Therefore, the solutions to the equation are:
- x + 2y - 3z = 0
- x² + 4y² + 9z² - 2xy + 3xz - 6yz = 0
Example 2: Finding the Volume of a Tetrahedron
Let's say we have a tetrahedron with side lengths a, b, and c. The volume of this tetrahedron can be expressed as:
V = (1/6)√(a³ + b³ + c³ - 3abc)
Using the factorization, we can rewrite the volume as:
V = (1/6)√[(a + b + c)(a² + b² + c² - ab - ac - bc)]
This expression allows us to calculate the volume of the tetrahedron directly from the lengths of its edges.
Conclusion
The factorization of a³ + b³ + c³ - 3abc into a product of polynomials is a remarkable result in algebra. It offers a powerful tool for simplifying expressions, solving equations, and exploring connections between different mathematical fields. The symmetry, roots, and geometric interpretation of the factorization make it a fascinating subject for further study and exploration. This factorization continues to play a vital role in various fields, contributing to our understanding of mathematics and its applications. The ability to factor a³ + b³ + c³ - 3abc provides a testament to the elegance and interconnectedness of mathematical concepts, highlighting the power of factorization as a fundamental tool in algebraic manipulation.