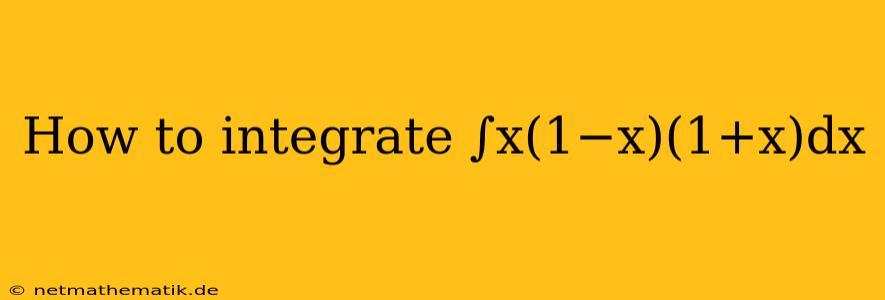The integral ∫x(1−x)(1+x)dx presents a straightforward example of integrating a polynomial function. This integral can be tackled using basic integration rules and algebraic manipulation. Let's break down the process step-by-step, exploring the different methods and insights involved.
Expanding the integrand
The initial step involves simplifying the integrand by expanding the product of the factors. We can use the difference of squares pattern: (1-x)(1+x) = 1 - x². This gives us:
∫x(1−x)(1+x)dx = ∫x(1 - x²) dx
Distributing the x term
Next, we distribute the 'x' term inside the integral:
∫x(1 - x²) dx = ∫(x - x³) dx
Applying the Power Rule
Now, we can directly apply the power rule of integration:
∫uⁿ du = (uⁿ⁺¹ / (n+1)) + C (where n ≠ -1)
Applying this to each term in the integral:
∫x dx = x²/2 + C₁ ∫x³ dx = x⁴/4 + C₂
Combining these results with the constants of integration:
∫(x - x³) dx = x²/2 - x⁴/4 + C
where C = C₁ + C₂
Alternative Method: Integration by Substitution
While expanding the integrand and applying the power rule is a straightforward method, we can also solve this integral using integration by substitution.
Let's define:
u = 1 - x²
Then:
du = -2x dx
Solving for 'x dx':
x dx = -du/2
Substituting these into the original integral:
∫x(1 - x²) dx = ∫u * (-du/2)
Now, we have a simpler integral:
-1/2 ∫u du
Applying the power rule:
-1/2 (u²/2) + C
Substituting back u = 1 - x²:
-1/4 (1 - x²)² + C
Expanding this:
-1/4 (1 - 2x² + x⁴) + C
Simplifying:
-1/4 + x²/2 - x⁴/4 + C
This result is equivalent to the one we obtained earlier, demonstrating the versatility of integration techniques.
Understanding the Solution
The integral ∫x(1−x)(1+x)dx represents the area under the curve of the function y = x(1−x)(1+x) between a specified interval. The solution we arrived at, x²/2 - x⁴/4 + C, represents a family of functions whose derivatives are equal to the original integrand. The constant of integration, C, indicates that there are infinitely many such functions, each shifted vertically by a different constant value.
Applications of Integrating Polynomials
Integrating polynomials has widespread applications across various fields:
- Physics: Finding the displacement of an object given its velocity function.
- Engineering: Calculating the volume of solids of revolution.
- Economics: Determining the total cost or revenue given marginal cost or revenue functions.
- Statistics: Computing the probability of events using probability density functions.
Conclusion
The integral ∫x(1−x)(1+x)dx provides a basic example of integrating a polynomial function. By expanding the integrand, applying the power rule, or utilizing integration by substitution, we arrive at a solution that represents the area under the curve of the integrand. Understanding integration of polynomials is fundamental in various fields, enabling us to model and solve real-world problems.