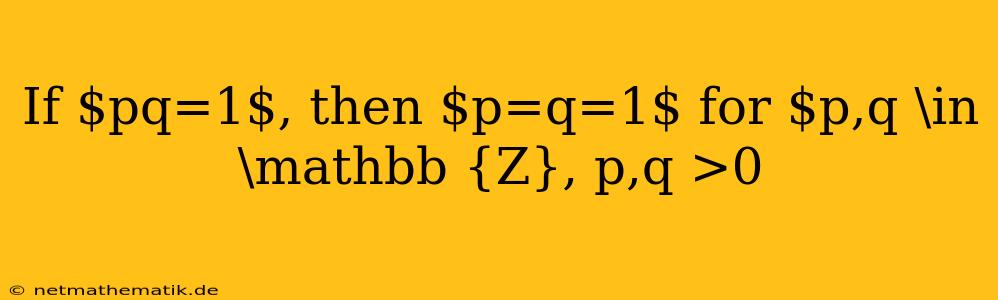The statement "If $pq=1$, then $p=q=1$ for $p,q \in \mathbb {Z}, p,q >0${content}quot; is a fundamental concept in mathematics, particularly in the realm of number theory and algebra. This statement asserts that if the product of two positive integers is equal to 1, then both integers must be equal to 1. This seemingly simple statement has significant implications and plays a crucial role in understanding the properties of integers and their relationships. In this article, we will delve into the proof of this statement, explore its applications, and examine its significance within the broader mathematical landscape.
Proof of the Statement
To prove that if $pq=1$, then $p=q=1$ for $p,q \in \mathbb{Z}, p,q >0$, we will employ a proof by contradiction. Let's assume, for the sake of contradiction, that either $p$ or $q$ is not equal to 1. Without loss of generality, let's assume that $p \neq 1$.
Since $p$ is a positive integer and $p \neq 1$, it follows that $p > 1$. Now, consider the product $pq$. Since $p > 1$, we have $pq > q$. However, we are given that $pq = 1$. This leads to the contradiction that $1 > q$. Since $q$ is a positive integer, it cannot be less than 1. Therefore, our initial assumption that $p \neq 1$ must be false. Consequently, we must have $p=1$.
Similarly, we can repeat the same argument for $q$. If $q \neq 1$, then $q > 1$, leading to $pq > p = 1$, which contradicts the given condition $pq = 1$. Hence, we must have $q = 1$.
Therefore, we have proven that if $pq=1$, then $p=q=1$ for $p,q \in \mathbb{Z}, p,q >0$.
Applications of the Statement
The statement "If $pq=1$, then $p=q=1$ for $p,q \in \mathbb{Z}, p,q >0${content}quot; has wide-ranging applications in various areas of mathematics, including:
1. Number Theory:
- Finding the Multiplicative Inverse: In number theory, the concept of multiplicative inverse is crucial. For any non-zero integer $p$, its multiplicative inverse is the integer $q$ such that $pq = 1$. This statement directly implies that the only positive integer with a multiplicative inverse equal to itself is 1.
- Divisibility: This statement is fundamental in understanding divisibility. If $p$ and $q$ are positive integers and $pq = 1$, then both $p$ and $q$ divide 1. This highlights the unique relationship between 1 and its divisors.
2. Algebra:
- Simplifying Equations: In algebraic manipulations, this statement is often used to simplify equations involving products of variables. If the product of two variables is equal to 1, then both variables must be equal to 1, allowing for further simplification.
- Solving Equations: This statement plays a role in solving equations involving products of variables. If an equation has a product of variables equal to 1, then by applying this statement, we can deduce that both variables must be equal to 1, which can assist in finding a solution.
3. Abstract Algebra:
- Group Theory: In abstract algebra, particularly in group theory, this statement is related to the concept of the identity element. In a group, the identity element is the unique element that, when multiplied by any other element, results in that element. This statement demonstrates that 1 acts as the identity element in the multiplicative group of positive integers.
Significance of the Statement
The statement "If $pq=1$, then $p=q=1$ for $p,q \in \mathbb{Z}, p,q >0${content}quot; is a fundamental building block in understanding the properties of integers and their multiplicative relationships. Its significance lies in its ability to:
- Define the Concept of Unity: This statement highlights the uniqueness of the number 1 in the set of positive integers. It is the only positive integer that is both a divisor and a multiple of itself.
- Establish the Inverse Property: The statement directly implies the existence of a multiplicative inverse for positive integers, where the inverse is equal to the original integer only when the integer is 1.
- Provide a Foundation for Higher Mathematics: This seemingly simple statement forms a foundation for many more complex mathematical concepts and theorems. It is used in proving various theorems and developing further mathematical theories.
Conclusion
The statement "If $pq=1$, then $p=q=1$ for $p,q \in \mathbb{Z}, p,q >0${content}quot; is a fundamental truth in mathematics that underscores the uniqueness of the number 1 in the set of positive integers. Its applications extend across various areas of mathematics, highlighting its importance in understanding the properties of integers and their multiplicative relationships. As a foundational concept, it plays a crucial role in developing more complex mathematical theories and solving intricate problems in various fields of study. By understanding and appreciating this statement, we gain a deeper insight into the intricate world of mathematics and its underlying principles.