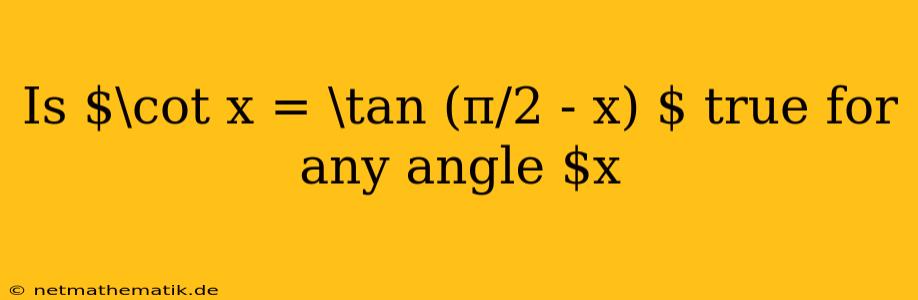The trigonometric identity $\cot x = \tan (π/2 - x)$ is a fundamental relationship that arises from the complementary angle relationships in trigonometry. This identity holds true for any angle $x$, except for angles where either $\cot x$ or $\tan (π/2 - x)$ is undefined. In this article, we will explore the validity of this identity, delve into its derivation, and illustrate its application with examples.
Understanding the Identity
The identity $\cot x = \tan (π/2 - x)$ establishes a connection between the cotangent and tangent functions. It states that the cotangent of an angle $x$ is equal to the tangent of the complementary angle, which is $π/2 - x$. This identity is particularly useful when dealing with trigonometric problems involving both cotangent and tangent functions, as it allows us to express one in terms of the other.
Visualizing the Identity
To visualize the identity, consider a right triangle with angles $x$, $π/2 - x$, and a right angle. The sides opposite and adjacent to angle $x$ are denoted as $opposite$ and $adjacent$, respectively. Similarly, the sides opposite and adjacent to angle $π/2 - x$ are denoted as $adjacent$ and $opposite$, respectively.
!%7B%3A%7D%20%5C%5C%26%5Ctext%7BAdjacent to }x%7B%3A%7D%26%5Ctext%7BOpposite to }(%5Cfrac%7B%5Cpi%7D%7B2%7D-x)%7B%3A%7D%20%5Cend%7Baligned%7D)
From the definitions of cotangent and tangent, we have:
- $\cot x = \frac{adjacent}{opposite}$
- $\tan (π/2 - x) = \frac{opposite}{adjacent}$
Since the adjacent side for angle $x$ is the opposite side for angle $π/2 - x$ and vice versa, we can see that the expressions for $\cot x$ and $\tan (π/2 - x)$ are reciprocals of each other, confirming the identity.
Derivation of the Identity
The identity $\cot x = \tan (π/2 - x)$ can be derived using the trigonometric definitions and the complementary angle relationships.
1. Starting with the definition of cotangent:
$\cot x = \frac{1}{\tan x}$
2. Expressing tangent in terms of sine and cosine:
$\cot x = \frac{1}{\frac{\sin x}{\cos x}} = \frac{\cos x}{\sin x}$
3. Applying the complementary angle relationships:
$\cos (π/2 - x) = \sin x$ and $\sin (π/2 - x) = \cos x$
4. Substituting the complementary angle relationships in the expression for cotangent:
$\cot x = \frac{\sin (π/2 - x)}{\cos (π/2 - x)}$
5. Recognizing the definition of tangent:
$\cot x = \tan (π/2 - x)$
Therefore, we have derived the identity $\cot x = \tan (π/2 - x)$ using the fundamental trigonometric definitions and relationships.
Applications of the Identity
The identity $\cot x = \tan (π/2 - x)$ has various applications in trigonometry and related fields. Some common applications include:
- Simplifying trigonometric expressions: The identity can be used to simplify expressions involving both cotangent and tangent functions. For instance, if we have an expression like $\frac{\cot x + \tan x}{1 - \cot x \tan x}$, we can substitute $\cot x = \tan (π/2 - x)$ to simplify it.
- Solving trigonometric equations: The identity can help solve trigonometric equations by transforming them into equivalent equations that are easier to solve. For example, if we have the equation $\cot x = 2$, we can rewrite it as $\tan (π/2 - x) = 2$ and then solve for $x$.
- Deriving other trigonometric identities: The identity can be used as a starting point to derive other trigonometric identities. For instance, by combining this identity with other known identities, we can derive expressions for $\csc x$, $\sec x$, and other trigonometric functions.
Examples
Let's illustrate the application of the identity with some examples.
Example 1: Simplifying a trigonometric expression
Simplify the expression $\frac{\cot x + \tan x}{1 - \cot x \tan x}$ using the identity $\cot x = \tan (π/2 - x)$.
Solution:
Substituting $\cot x = \tan (π/2 - x)$, we get:
$\frac{\cot x + \tan x}{1 - \cot x \tan x} = \frac{\tan (π/2 - x) + \tan x}{1 - \tan (π/2 - x) \tan x}$
Using the tangent addition formula, $\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B}$, we can simplify the expression:
$\frac{\tan (π/2 - x) + \tan x}{1 - \tan (π/2 - x) \tan x} = \tan [(π/2 - x) + x] = \tan (π/2) = undefined$
Therefore, the simplified expression is undefined.
Example 2: Solving a trigonometric equation
Solve the equation $\cot x = 2$ using the identity $\cot x = \tan (π/2 - x)$.
Solution:
Substituting $\cot x = \tan (π/2 - x)$, we get:
$\tan (π/2 - x) = 2$
Taking the inverse tangent of both sides, we get:
$π/2 - x = \arctan 2$
Solving for $x$, we get:
$x = π/2 - \arctan 2$
Therefore, the solution to the equation $\cot x = 2$ is $x = π/2 - \arctan 2$.
Conclusion
The identity $\cot x = \tan (π/2 - x)$ is a powerful tool in trigonometry, connecting the cotangent and tangent functions through complementary angles. It provides a versatile means to simplify expressions, solve equations, and derive other trigonometric identities. By understanding the relationship between these functions and their complementary angles, we can enhance our understanding of trigonometric concepts and applications.