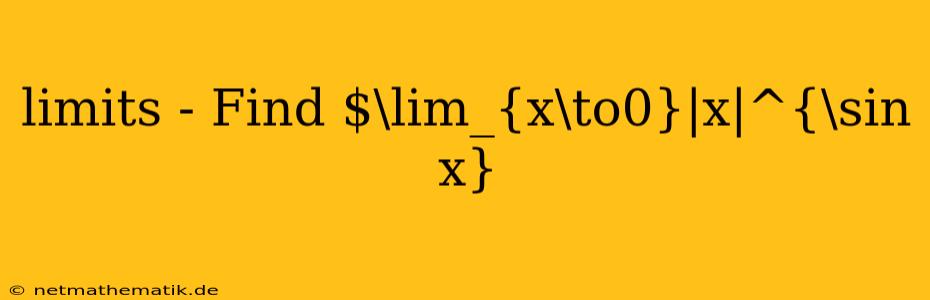Evaluating limits can often be a challenging task, especially when dealing with functions that involve both trigonometric and absolute value components. One such example is the limit of $|x|^{\sin x}$ as $x$ approaches zero. This expression presents a unique challenge because it involves the indeterminate form $0^0$, a scenario that requires careful analysis and application of appropriate techniques. In this article, we will delve into the intricacies of finding $\lim_{x\to0}|x|^{\sin x}$, exploring various approaches and providing a step-by-step solution to unveil the true value of this limit.
Analyzing the Indeterminate Form
As $x$ approaches zero, both the base, $|x|$, and the exponent, $\sin x$, approach zero. This creates an indeterminate form $0^0$, which is a classic case of ambiguity in mathematics. Direct substitution cannot determine the limit's value, necessitating the use of techniques that circumvent this ambiguity.
Employing L'Hôpital's Rule
One common technique to handle indeterminate forms is L'Hôpital's Rule. However, directly applying L'Hôpital's Rule to $|x|^{\sin x}$ is not immediately feasible. L'Hôpital's Rule is designed for quotients of functions, not for functions raised to a power. To use L'Hôpital's Rule, we need to rewrite the expression in a form suitable for the rule's application.
Transforming the Limit
The key lies in utilizing the properties of logarithms. By taking the natural logarithm of both sides of the original limit expression, we can transform the expression into a more manageable form.
Let $L = \lim_{x\to0}|x|^{\sin x}$. Then,
$\ln L = \ln \left(\lim_{x\to0}|x|^{\sin x}\right)$
Using the properties of limits and logarithms, we can rewrite this as:
$\ln L = \lim_{x\to0} \ln (|x|^{\sin x}) = \lim_{x\to0} \sin x \ln |x|$
We have now transformed the original limit into an expression that is more amenable to L'Hôpital's Rule.
Applying L'Hôpital's Rule
The expression $\lim_{x\to0} \sin x \ln |x|$ is still in an indeterminate form, but it is now a product of two functions. To use L'Hôpital's Rule, we need to express it as a quotient. We can achieve this by rewriting it as:
$\lim_{x\to0} \sin x \ln |x| = \lim_{x\to0} \frac{\ln |x|}{\frac{1}{\sin x}}$
Now, both the numerator and denominator approach infinity as $x$ approaches zero. This allows us to apply L'Hôpital's Rule. Taking the derivative of both the numerator and denominator, we obtain:
$\lim_{x\to0} \frac{\ln |x|}{\frac{1}{\sin x}} = \lim_{x\to0} \frac{\frac{1}{x}}{-\frac{\cos x}{\sin^2 x}} = \lim_{x\to0} -\frac{\sin^2 x}{x \cos x}$
Again, the resulting limit is in the indeterminate form $\frac{0}{0}$. Applying L'Hôpital's Rule once more, we get:
$\lim_{x\to0} -\frac{\sin^2 x}{x \cos x} = \lim_{x\to0} -\frac{2 \sin x \cos x}{\cos x - x \sin x}$
Finally, as $x$ approaches zero, this limit evaluates to:
$\lim_{x\to0} -\frac{2 \sin x \cos x}{\cos x - x \sin x} = -\frac{2 \cdot 0 \cdot 1}{1 - 0 \cdot 0} = 0$
Finding the Original Limit
We have now found that $\ln L = 0$. To determine the original limit, $L$, we need to take the exponential of both sides:
$L = e^{\ln L} = e^0 = 1$
Conclusion
Therefore, the limit of $|x|^{\sin x}$ as $x$ approaches zero is equal to 1. This solution highlights the importance of transforming limit expressions to utilize techniques like L'Hôpital's Rule effectively. By carefully manipulating the expression, we can overcome the initial ambiguity of the indeterminate form and arrive at a definitive value for the limit. This process illustrates the power of logarithmic manipulation and calculus in solving complex limit problems.