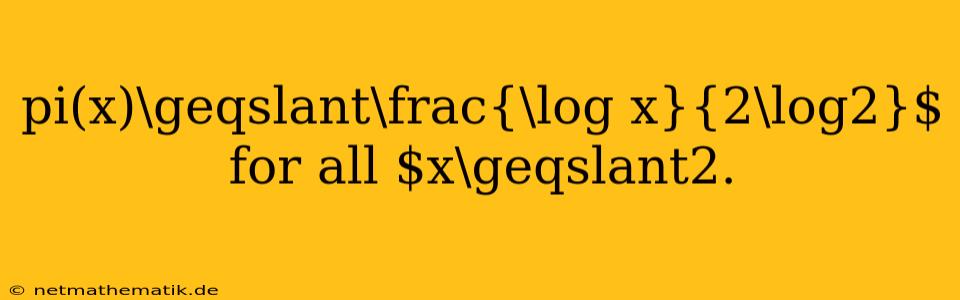The inequality $\pi(x)\geqslant\frac{\log x}{2\log2}$ for all $x\geqslant2$ is a fundamental result in number theory that provides a lower bound for the number of prime numbers less than or equal to a given number. This inequality, often referred to as the Chebyshev's inequality, plays a crucial role in understanding the distribution of prime numbers and is a key ingredient in proving the Prime Number Theorem. In this article, we will delve into the proof of Chebyshev's inequality, explore its significance, and discuss its connection to other important results in number theory.
Chebyshev's Inequality: A Lower Bound for Prime Counting Function
The prime counting function, denoted by $\pi(x)$, represents the number of prime numbers less than or equal to a given number $x$. Understanding the behavior of $\pi(x)$ is a central problem in number theory. Chebyshev's inequality establishes a lower bound for $\pi(x)$ for all $x\geqslant2$. This inequality states that:
$\pi(x)\geqslant\frac{\log x}{2\log2}$ for all $x\geqslant2$
In simpler terms, this inequality suggests that the number of primes less than or equal to $x$ is at least as large as $\frac{\log x}{2\log2}$. This result provides a crucial insight into the distribution of prime numbers, suggesting that there are "sufficiently many" primes up to any given number.
Proof of Chebyshev's Inequality
The proof of Chebyshev's inequality relies on clever combinatorial arguments and the properties of binomial coefficients. Here's a sketch of the proof:
- Bounding the Central Binomial Coefficient: We begin by examining the central binomial coefficient $\binom{2n}{n}$. Using the factorial representation of binomial coefficients, we can write:
$\binom{2n}{n} = \frac{(2n)!}{n!n!} = \frac{2n(2n-1)\cdots(n+1)}{n(n-1)\cdots1} \geqslant 2^n$
The inequality arises from the fact that each term in the numerator is greater than or equal to the corresponding term in the denominator.
-
Prime Factorization: Next, we consider the prime factorization of $\binom{2n}{n}$. Every prime number $p$ less than or equal to $2n$ appears in the prime factorization of $(2n)!$ at least once. Since $p$ also appears in the prime factorization of $n!$, its exponent in $\binom{2n}{n}$ is at most the difference between its exponents in $(2n)!$ and $n!$. This difference is bounded above by $\log_{p}(2n) - \log_{p}(n) = \log_{p}(2)$.
-
Combining the Bounds: Combining the bounds from steps 1 and 2, we obtain:
$\binom{2n}{n} \leqslant \prod_{p \leqslant 2n} p^{\log_{p}(2)} = 2^{\sum_{p\leqslant 2n} \log_{p}(2)} = 2^{\log_{2}(\prod_{p\leqslant 2n} p)}$
Taking the logarithm of both sides, we get:
$\log \binom{2n}{n} \leqslant \log_{2}(\prod_{p\leqslant 2n} p)$
Since $\log \binom{2n}{n} \geqslant n\log 2$, we can conclude that:
$n\log2 \leqslant \log_{2}(\prod_{p\leqslant 2n} p)$
This inequality implies that the product of all primes less than or equal to $2n$ is at least $2^n$.
- Final Steps: To establish Chebyshev's inequality, we need to relate the product of primes to $\pi(2n)$. Since $\pi(2n)$ is the number of primes less than or equal to $2n$, we have:
$\prod_{p\leqslant 2n} p \leqslant (2n)^{\pi(2n)}$
Combining this inequality with the previous one, we get:
$2^n \leqslant (2n)^{\pi(2n)}$
Taking the logarithm of both sides and rearranging, we obtain:
$\pi(2n) \geqslant \frac{n\log2}{\log(2n)} = \frac{\log2n}{2\log2}$
Finally, substituting $x = 2n$ gives us:
$\pi(x) \geqslant \frac{\log x}{2\log2}$ for all $x\geqslant2$
This completes the proof of Chebyshev's inequality.
Significance of Chebyshev's Inequality
Chebyshev's inequality is a powerful result that has several important implications:
-
Lower Bound for Prime Density: It provides a concrete lower bound for the density of prime numbers. This lower bound, while not asymptotically tight, demonstrates that prime numbers are not "sparse" but rather become increasingly frequent as we move towards larger numbers.
-
Connection to the Prime Number Theorem: Chebyshev's inequality is a key step in the proof of the Prime Number Theorem, which states that $\pi(x)$ is asymptotically equivalent to $\frac{x}{\log x}$. This theorem is one of the most important results in number theory, providing a precise estimate for the distribution of prime numbers.
-
Applications in Cryptography: Chebyshev's inequality has implications in cryptography, particularly in the context of generating large prime numbers for cryptographic algorithms. It guarantees the existence of "sufficiently many" primes in a given range, which is essential for secure encryption and decryption.
Further Explorations: Beyond Chebyshev's Inequality
While Chebyshev's inequality provides a fundamental lower bound for $\pi(x)$, it is not the tightest possible bound. More refined estimates for the prime counting function have been established using more sophisticated methods, leading to the development of the Prime Number Theorem.
The Prime Number Theorem, which states that $\lim_{x \to \infty} \frac{\pi(x)}{x/\log x} = 1$, provides a precise asymptotic formula for the distribution of prime numbers. This theorem has profound implications for our understanding of prime numbers and their distribution.
Furthermore, Chebyshev's inequality and the Prime Number Theorem have inspired further research into the distribution of prime numbers, leading to the development of advanced techniques and theories such as the Riemann Hypothesis, which conjectures a relationship between the distribution of prime numbers and the zeros of the Riemann zeta function.
Conclusion
Chebyshev's inequality, stating that $\pi(x)\geqslant\frac{\log x}{2\log2}$ for all $x\geqslant2$, is a foundational result in number theory. It provides a crucial lower bound for the number of primes less than or equal to a given number, demonstrating the "abundance" of prime numbers. The proof of Chebyshev's inequality relies on combinatorial arguments and properties of binomial coefficients, highlighting the power of these techniques in tackling problems in number theory. Its significance extends beyond providing a lower bound, as it serves as a stepping stone towards the Prime Number Theorem and has implications in various areas like cryptography. Chebyshev's inequality and the subsequent development of the Prime Number Theorem stand as testaments to the enduring fascination with prime numbers and the depth of number theory.