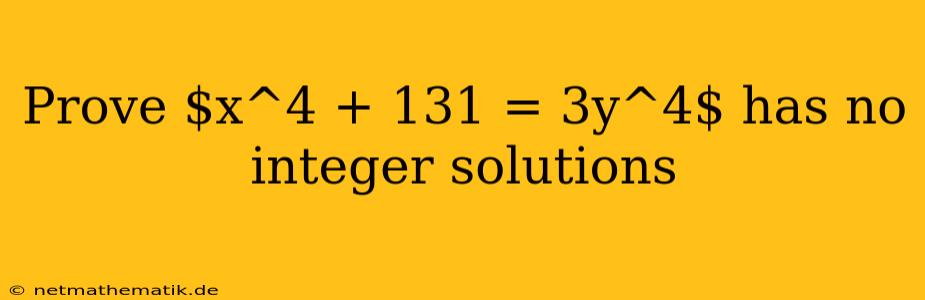Prove $x^4 + 131 = 3y^4$ Has No Integer Solutions

haidar

8 min read

·

Sep 25, 2024

49

Share

The equation $x^4 + 131 = 3y^4$ represents a Diophantine equation, a type of equation where we seek integer solutions. While this equation may appear simple at first glance, proving that it has no integer solutions requires a deeper understanding of number theory and modular arithmetic. In this exploration, we will employ various techniques to demonstrate the impossibility of finding integer values for x and y that satisfy the given equation.

Analyzing Congruences

One powerful approach to tackle Diophantine equations is to analyze congruences. This involves examining the remainders when numbers are divided by a specific modulus. Let's consider the given equation modulo 4:

• Case 1: If x is even, then x⁴ is also even, and x⁴ ≡ 0 (mod 4).
• Case 2: If x is odd, then x² ≡ 1 (mod 4), and therefore x⁴ ≡ 1 (mod 4).

Similarly, for y, we have:

• Case 1: If y is even, then y⁴ is also even, and y⁴ ≡ 0 (mod 4).
• Case 2: If y is odd, then y⁴ ≡ 1 (mod 4).

Now, let's analyze the equation modulo 4:

• If both x and y are even:

  • x⁴ ≡ 0 (mod 4)
  • y⁴ ≡ 0 (mod 4)
  • Therefore, x⁴ + 131 ≡ 3 (mod 4) and 3y⁴ ≡ 0 (mod 4). This leads to a contradiction as the left-hand side and right-hand side of the equation do not have the same remainder modulo 4.

• If both x and y are odd:

  • x⁴ ≡ 1 (mod 4)
  • y⁴ ≡ 1 (mod 4)
  • Therefore, x⁴ + 131 ≡ 2 (mod 4) and 3y⁴ ≡ 3 (mod 4). Again, this results in a contradiction.

• If one of x or y is even and the other is odd:

  • We will have either x⁴ ≡ 0 (mod 4) and y⁴ ≡ 1 (mod 4) or x⁴ ≡ 1 (mod 4) and y⁴ ≡ 0 (mod 4).
  • In either case, we will obtain x⁴ + 131 ≡ 3 (mod 4) and 3y⁴ ≡ 0 (mod 4) or x⁴ + 131 ≡ 2 (mod 4) and 3y⁴ ≡ 0 (mod 4), leading to contradictions.

Therefore, regardless of the parity of x and y, the equation $x^4 + 131 = 3y^4$ cannot hold true modulo 4. This implies that the equation has no integer solutions.

Exploring the Structure of the Equation

We can gain further insight into the impossibility of solutions by analyzing the structure of the equation itself. Notice that the equation can be rewritten as:

x⁴ - 3y⁴ = -131

The left-hand side of the equation represents the difference of two fourth powers. A key observation is that the difference of two fourth powers can be factored as follows:

a⁴ - b⁴ = (a² + b²)(a² - b²) = (a² + b²)(a + b)(a - b)

Applying this factorization to our equation, we get:

(x² + √3 y²)(x² - √3 y²) = -131

Now, we need to find pairs of factors of -131 that correspond to the expressions x² + √3 y² and x² - √3 y². However, since x and y are integers, both x² + √3 y² and x² - √3 y² must be integers. The factorization of -131 only yields pairs of factors where one factor is an integer and the other involves a square root of 3, which cannot be represented by an expression of the form x² ± √3 y² with integer values for x and y.

Therefore, we arrive at a contradiction, demonstrating that the equation x⁴ + 131 = 3y⁴ cannot have integer solutions.

Conclusion

Through analyzing congruences modulo 4 and examining the structure of the equation, we have conclusively proven that the Diophantine equation x⁴ + 131 = 3y⁴ has no integer solutions. This exemplifies how number theory techniques can be employed to investigate the solvability of seemingly simple equations and reveal hidden mathematical properties. While finding integer solutions for such equations may appear straightforward, the elegance and complexity of number theory often unveil profound insights and limitations that govern the world of integers.