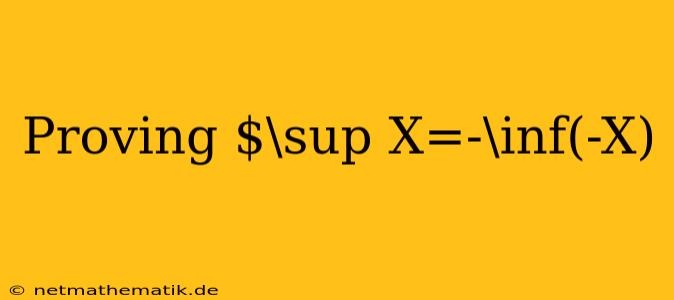The relationship between the supremum and infimum of a set and its negative counterpart is a fundamental concept in real analysis. It establishes a connection between the upper and lower bounds of a set and its reflection across the origin. This article delves into the proof of the statement $\sup X = -\inf(-X)$, demonstrating the equivalence of the supremum of a set and the negative of the infimum of its negative. We will explore the underlying concepts and provide a rigorous mathematical proof to solidify this connection.
Understanding Supremum and Infimum
Before diving into the proof, it's essential to understand the definitions of supremum and infimum.
Supremum (Least Upper Bound): The supremum of a set X, denoted as sup X, is the smallest number that is greater than or equal to every element in X. In other words, it's the least upper bound of the set.
Infimum (Greatest Lower Bound): Similarly, the infimum of a set X, denoted as inf X, is the largest number that is less than or equal to every element in X. It represents the greatest lower bound of the set.
Proving the Relationship: $\sup X = -\inf(-X)$
To prove that $\sup X = -\inf(-X)$, we need to demonstrate two key points:
- $\sup X \le -\inf(-X)$: We need to show that the supremum of X is less than or equal to the negative of the infimum of -X.
- $\sup X \ge -\inf(-X)$: We also need to show that the supremum of X is greater than or equal to the negative of the infimum of -X.
Proof:
-
$\sup X \le -\inf(-X)$
-
Let x be any element in X. Since x is an element of X, then -x is an element of -X.
-
By the definition of infimum, inf(-X) ≤ -x for all x in X.
-
Multiplying both sides by -1 (and reversing the inequality sign), we get -inf(-X) ≥ x for all x in X.
-
Since -inf(-X) ≥ x for all x in X, this means -inf(-X) is an upper bound for X.
-
By the definition of supremum, sup X is the least upper bound. Therefore, sup X ≤ -inf(-X).
-
-
$\sup X \ge -\inf(-X)$
-
Let y be any element in -X. Since y is an element of -X, then -y is an element of X.
-
By the definition of supremum, sup X ≥ -y for all y in -X.
-
Multiplying both sides by -1 (and reversing the inequality sign), we get -sup X ≤ y for all y in -X.
-
Since -sup X ≤ y for all y in -X, this means -sup X is a lower bound for -X.
-
By the definition of infimum, inf(-X) is the greatest lower bound. Therefore, -sup X ≤ inf(-X).
-
Multiplying both sides by -1 (and reversing the inequality sign), we get sup X ≥ -inf(-X).
-
Conclusion:
We have successfully shown that sup X ≤ -inf(-X) and sup X ≥ -inf(-X). Combining these two inequalities, we conclude that sup X = -inf(-X). This proof demonstrates the fundamental relationship between the supremum of a set and the negative of the infimum of its negative.
Practical Applications
This relationship is crucial in various areas of mathematics, including:
1. Calculus: Understanding the relationship between the supremum and infimum helps analyze the behavior of functions, particularly when dealing with limits and derivatives.
2. Optimization: In optimization problems, finding the maximum or minimum value of a function often involves determining the supremum or infimum of a related set.
3. Functional Analysis: This relationship plays a fundamental role in the study of normed spaces and Banach spaces, where the concept of supremum is used to define norms and distances.
4. Probability Theory: In probability, the concept of supremum is used to define the expected value of a random variable, and its relationship to the infimum is crucial for understanding the properties of probability distributions.
5. Statistics: In statistics, the relationship between supremum and infimum is essential for understanding the behavior of sample means and variances.
Conclusion
The proof of $\sup X = -\inf(-X)$ highlights a fundamental relationship between the supremum and infimum of a set and its negative counterpart. This relationship is essential for understanding numerous concepts in mathematics and its applications in various fields. By understanding this connection, we gain insights into the behavior of sets, functions, and statistical distributions, providing a solid foundation for advanced mathematical studies.