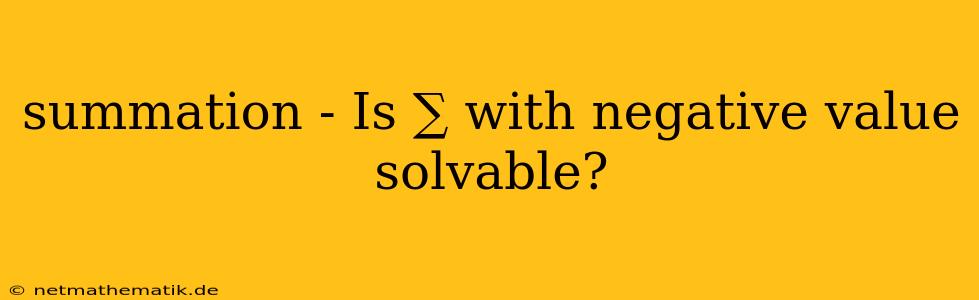The concept of summation, denoted by the symbol ∑ (sigma), is a fundamental tool in mathematics used to represent the sum of a series of numbers. While summations are typically associated with positive values, the question arises: Can a summation with a negative value be solved? The answer is yes, but understanding how negative values influence summations requires a deeper exploration of the concept.
Understanding Summation and Its Applications
Summation is a powerful mathematical tool used in various fields like calculus, statistics, and computer science. It allows us to concisely represent the sum of a sequence of numbers. A summation is typically expressed as:
∑_(i=m)^n a_i
Where:
- ∑ (sigma) represents the summation symbol.
- i is the index of summation.
- m is the lower limit of summation, the starting value of the index.
- n is the upper limit of summation, the ending value of the index.
- a_i is the general term of the sequence, which can be any expression depending on the index i.
For example: The sum of the first five natural numbers can be expressed as:
∑_(i=1)^5 i = 1 + 2 + 3 + 4 + 5 = 15
Summation with Negative Values
While summations are often encountered with positive values, negative values can also be included within the summation. The process of solving a summation with negative values is similar to that with positive values. The key is to properly interpret the sign of each term within the summation.
Here's a breakdown:
-
Negative index: If the index of summation is negative, the sequence will iterate through negative values. For example, ∑_(i=-3)^1 i would sum the terms -3, -2, -1, 0, and 1.
-
Negative term: If the general term a_i contains a negative value, it will contribute negatively to the overall sum. For example, ∑_(i=1)^3 -i would sum the terms -1, -2, and -3, resulting in -6.
-
Negative upper and lower limits: If the upper limit of summation is less than the lower limit, the summation will be empty and its value will be zero. For example, ∑_(i=3)^1 i = 0.
Solving Summations with Negative Values
The process of solving a summation with negative values involves evaluating the general term a_i for each value of the index i within the specified range and then adding the resulting terms.
Example:
Let's calculate the summation ∑_(i=-2)^2 (i^2 - 2).
-
Step 1: Evaluate the general term for each index value.
- For i = -2: (-2)^2 - 2 = 2
- For i = -1: (-1)^2 - 2 = -1
- For i = 0: (0)^2 - 2 = -2
- For i = 1: (1)^2 - 2 = -1
- For i = 2: (2)^2 - 2 = 2
-
Step 2: Add the resulting terms: 2 + (-1) + (-2) + (-1) + 2 = 0
Therefore, ∑_(i=-2)^2 (i^2 - 2) = 0
Applications of Summation with Negative Values
Summations with negative values find applications in various fields.
-
Statistics: In probability distributions, negative values can represent deviations from the mean, and summations involving these negative values are used to calculate important statistical measures like variance.
-
Calculus: The concept of definite integrals is closely related to summation. Negative values in the integrand can contribute to the area under the curve, which can be calculated using summation.
-
Computer Science: Summations are used extensively in algorithms and data structures. For example, in binary search, a summation with negative values can be used to calculate the position of an element in a sorted array.
Conclusion
Summation is a powerful mathematical concept that can be applied to both positive and negative values. The process of solving a summation with negative values involves evaluating the general term for each index within the given range and adding the resulting terms. While negative values may appear complex, they play a vital role in various fields, contributing to a deeper understanding of mathematical and scientific phenomena.