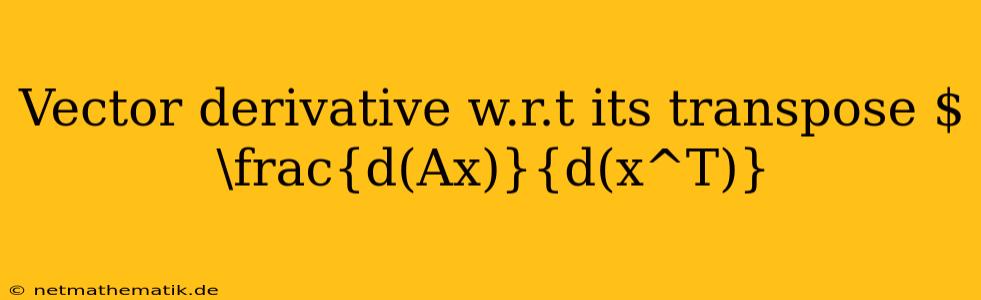The concept of a vector derivative with respect to its transpose, denoted as $\frac{d(Ax)}{d(x^T)}$, plays a crucial role in various fields, including optimization, machine learning, and control theory. This derivative, often referred to as the Jacobian matrix, is a fundamental tool for analyzing the relationship between a vector function and its input. In this article, we will delve into the mathematical definition and properties of the vector derivative with respect to its transpose, exploring its significance and applications in different contexts.
Understanding Vector Derivatives with Respect to Transpose
Before we delve into the definition and properties of $\frac{d(Ax)}{d(x^T)}$, it is essential to understand the concept of a vector derivative in general. A vector derivative describes the rate of change of a vector-valued function with respect to its input. In essence, it captures how the output vector changes in response to infinitesimal variations in the input vector.
The Jacobian Matrix: A Key Concept
The derivative of a vector function $f(x)$, where $x$ is a vector, is represented by the Jacobian matrix. Each element of the Jacobian matrix corresponds to the partial derivative of an element of the output vector with respect to an element of the input vector. Mathematically, if $f(x) = [f_1(x), f_2(x), ..., f_m(x)]^T$, then the Jacobian matrix is given by:
$\frac{df(x)}{dx} = \begin{bmatrix} \frac{\partial f_1(x)}{\partial x_1} & \frac{\partial f_1(x)}{\partial x_2} & ... & \frac{\partial f_1(x)}{\partial x_n} \ \frac{\partial f_2(x)}{\partial x_1} & \frac{\partial f_2(x)}{\partial x_2} & ... & \frac{\partial f_2(x)}{\partial x_n} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial f_m(x)}{\partial x_1} & \frac{\partial f_m(x)}{\partial x_2} & ... & \frac{\partial f_m(x)}{\partial x_n} \end{bmatrix}$
The Specific Case of $\frac{d(Ax)}{d(x^T)}$
Now, let's focus on the derivative of a vector function $Ax$ with respect to its transpose $x^T$, where $A$ is a constant matrix. This derivative is particularly useful in optimization problems where we need to find the optimal value of $x$ that minimizes or maximizes a function involving $Ax$.
The derivative $\frac{d(Ax)}{d(x^T)}$ is calculated by taking the partial derivative of each element of $Ax$ with respect to each element of $x^T$. Since $Ax$ is a vector, the derivative will be a matrix, known as the Jacobian matrix for $Ax$. Applying the rules of matrix differentiation, we obtain:
$\frac{d(Ax)}{d(x^T)} = \frac{d}{dx^T} \begin{bmatrix} a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n \ a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n \ \vdots \ a_{m1}x_1 + a_{m2}x_2 + ... + a_{mn}x_n \end{bmatrix} = A^T$
Therefore, the derivative of $Ax$ with respect to its transpose $x^T$ is simply the transpose of the matrix $A$. This result is straightforward and demonstrates the elegance of vector calculus in simplifying complex calculations.
Properties of the Derivative $\frac{d(Ax)}{d(x^T)}$
The derivative $\frac{d(Ax)}{d(x^T)}$ possesses several key properties that make it particularly useful in different applications. These properties include:
1. Linearity:
The derivative is linear with respect to both $A$ and $x$. This means that if $A$ and $B$ are constant matrices and $x$ and $y$ are vectors, then:
$\frac{d(A(x+y))}{d(x^T)} = A^T + B^T = \frac{d(Ax)}{d(x^T)} + \frac{d(By)}{d(x^T)}$
2. Symmetry:
If $A$ is a symmetric matrix, then the derivative is also symmetric. This property is a direct consequence of the fact that $A^T = A$ for symmetric matrices.
3. Chain Rule:
The chain rule applies to this derivative as well. If $f(x)$ is a function of $Ax$, then the derivative of $f(x)$ with respect to $x^T$ can be expressed as:
$\frac{df(x)}{dx^T} = \frac{df(x)}{d(Ax)} \frac{d(Ax)}{dx^T} = \frac{df(x)}{d(Ax)} A^T$
Applications of the Derivative $\frac{d(Ax)}{d(x^T)}$
The derivative $\frac{d(Ax)}{d(x^T)}$ finds wide application in various areas of mathematics, statistics, and engineering. Some notable applications include:
1. Optimization:
In optimization problems, we often need to find the optimal values of variables that minimize or maximize a given function. The derivative $\frac{d(Ax)}{d(x^T)}$ plays a crucial role in finding these optimal values. For example, in linear programming, the objective function is often expressed as $Ax$, and the derivative is used to determine the gradient of the objective function.
2. Machine Learning:
In machine learning, the derivative is used to train models by adjusting the parameters to minimize the error between predicted and actual values. For instance, in neural networks, the backpropagation algorithm utilizes the derivative to propagate error gradients through the network layers, enabling parameter updates.
3. Control Theory:
In control theory, the derivative is used to analyze the stability and performance of systems. The derivative of the state equation with respect to the input vector helps in determining the controllability and observability of the system.
Conclusion
The derivative of a vector function $Ax$ with respect to its transpose $x^T$, denoted as $\frac{d(Ax)}{d(x^T)}$, is a powerful mathematical tool with broad applications in various fields. Understanding its definition, properties, and applications provides a deeper understanding of vector calculus and its relevance to solving complex problems. From optimization and machine learning to control theory, this derivative plays a crucial role in advancing our understanding and solving real-world problems. Its significance stems from its ability to capture the relationship between a vector function and its input, enabling us to analyze and manipulate vector-valued functions efficiently.