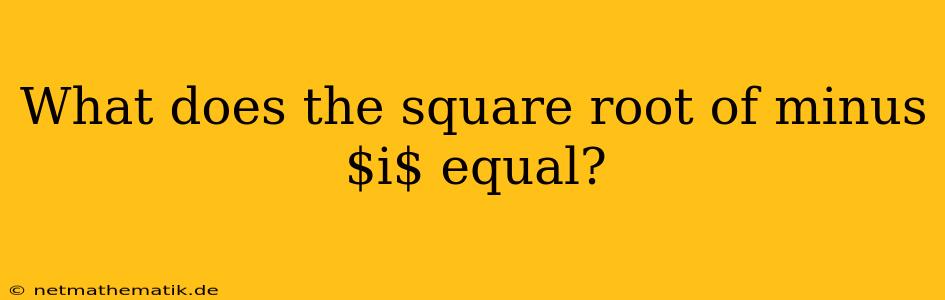The question of what the square root of negative $i$ equals delves into the fascinating world of complex numbers. While the square root of a negative real number like -1 is imaginary, represented by $i$, the square root of $-i$ itself becomes a complex number with both real and imaginary components. Let's explore how to find this solution.
Understanding Complex Numbers
Complex numbers are a fundamental concept in mathematics that extend the real number system. They are expressed in the form $a + bi$, where $a$ and $b$ are real numbers, and $i$ represents the imaginary unit, defined as the square root of -1: $i = \sqrt{-1}$.
The complex number $a + bi$ can be visualized as a point in the complex plane, where the real part ($a$) is plotted on the horizontal axis (the real axis) and the imaginary part ($b$) is plotted on the vertical axis (the imaginary axis). This graphical representation allows us to perform operations like addition, subtraction, multiplication, and division on complex numbers.
Finding the Square Root of -$i$
To find the square root of -$i$, we need to find a complex number $z$ such that $z^2 = -i$. Let's express $z$ in its general complex form:
$z = a + bi$
Squaring both sides, we get:
$z^2 = (a + bi)^2 = a^2 + 2abi + (bi)^2 = (a^2 - b^2) + 2abi$
We know that this must equal $-i$, which can be written as $0 - i$. Now we equate the real and imaginary parts:
- Real part: $a^2 - b^2 = 0$
- Imaginary part: $2ab = -1$
From the real part equation, we get $a^2 = b^2$, which means $a = b$ or $a = -b$.
Now, let's consider both possibilities:
Case 1: a = b
Substituting $a = b$ into the imaginary part equation, we get:
$2a^2 = -1$
This has no real solutions for $a$, so this case is not valid.
Case 2: a = -b
Substituting $a = -b$ into the imaginary part equation, we get:
$-2b^2 = -1$
Solving for $b$, we get:
$b^2 = \frac{1}{2}$
Therefore, $b = \frac{1}{\sqrt{2}}$ or $b = -\frac{1}{\sqrt{2}}$. Since $a = -b$, we have two possible solutions for $z$:
- Solution 1: $z_1 = -\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i$
- Solution 2: $z_2 = \frac{1}{\sqrt{2}} - \frac{1}{\sqrt{2}}i$
Verification
We can verify that these solutions are indeed square roots of $-i$ by squaring them:
- $z_1^2 = (-\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i)^2 = \frac{1}{2} - \frac{2}{\sqrt{2}}\frac{1}{\sqrt{2}}i + \frac{1}{2}i^2 = 0 - i = -i$
- $z_2^2 = (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{2}}i)^2 = \frac{1}{2} - \frac{2}{\sqrt{2}}\frac{1}{\sqrt{2}}i + \frac{1}{2}i^2 = 0 - i = -i$
Conclusion
Therefore, the square roots of $-i$ are:
- $-\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i$
- $\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{2}}i$
This demonstrates that even the seemingly simple operation of finding a square root can lead to fascinating results in the realm of complex numbers. The understanding of what does the square root of minus $i$ equal? highlights the power and beauty of complex numbers in extending mathematical concepts beyond the real number system.