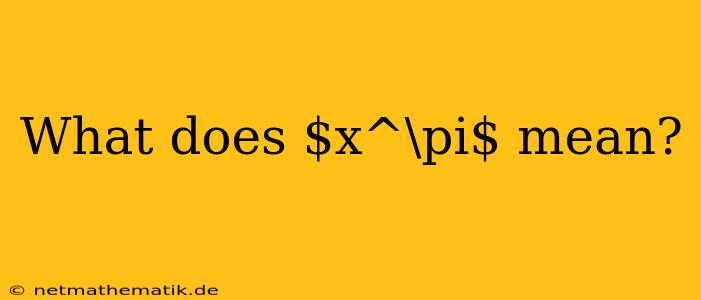The concept of raising a number to an irrational power like pi, denoted as $x^\pi$, might seem strange at first glance. After all, we are used to dealing with exponents that are whole numbers or rational fractions. However, the definition of exponentiation can be extended to include irrational exponents like pi, allowing us to understand and calculate such expressions. This extension is built upon the foundations of continuous functions and the concept of limits.
Understanding Exponentiation with Irrational Exponents
To comprehend the meaning of $x^\pi$, we need to understand how exponentiation works in general. For positive integers 'n', $x^n$ represents the product of 'n' copies of 'x':
$x^n = x \times x \times x \times ... \times x$ (n times)
For rational exponents of the form $m/n$, where 'm' and 'n' are integers, $x^{m/n}$ is defined as the 'n'th root of $x^m$:
$x^{m/n} = \sqrt[n]{x^m}$
However, $\pi$ is an irrational number, meaning it cannot be expressed as a ratio of two integers. This presents a challenge as we cannot directly use the above definitions.
The Power of Limits and Continuity
To address this, we turn to the concept of limits and continuous functions. We can approximate pi with a sequence of rational numbers that get increasingly closer to its true value. For example:
3, 3.1, 3.14, 3.141, 3.1415, ...
We can then calculate $x$ raised to each of these rational approximations. As the rational approximations get closer to pi, the resulting values of $x$ raised to those approximations will converge to a specific value. This limiting value is what we define as $x^\pi$.
Formal Definition Using Limits
Mathematically, we can express this using the limit notation:
$x^\pi = \lim_{n \to \infty} x^{r_n}$, where $r_n$ is a sequence of rational numbers approaching pi.
This definition implies that we can calculate $x^\pi$ with arbitrary precision by choosing a sufficiently accurate rational approximation of pi.
Applications of Irrational Exponents
The ability to raise a number to an irrational exponent has significant implications in various fields:
1. Calculus: The concept of limits is crucial for understanding derivatives and integrals. Irrational exponents appear in expressions like $x^\pi$, which can be differentiated and integrated using the rules of calculus.
2. Physics: Many physical phenomena involve exponential relationships described by irrational exponents. For example, radioactive decay is governed by an exponential function with a base of 'e' (Euler's number) raised to an irrational exponent.
3. Engineering: In fields like electrical engineering, irrational exponents are used to model phenomena like AC circuits and wave propagation.
4. Finance: The concept of compound interest involves exponential growth, which can be expressed using irrational exponents to model continuous compounding.
Conclusion
While raising a number to an irrational exponent like pi may seem counterintuitive at first, the concept is firmly grounded in mathematics. The use of limits and continuous functions allows us to extend the definition of exponentiation to irrational exponents, enabling us to calculate and understand expressions like $x^\pi$. This concept has far-reaching applications across various scientific and engineering disciplines, demonstrating the power of mathematical concepts to model complex phenomena.