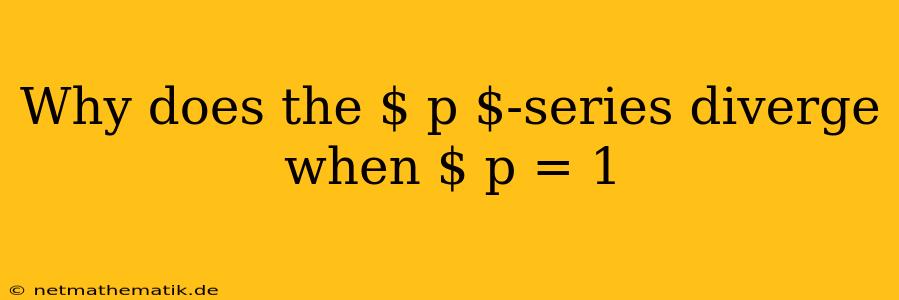The world of infinite series is filled with fascinating patterns and behaviors. One such series, the $p$-series, plays a crucial role in understanding convergence and divergence. This series takes the form of $\sum_{n=1}^\infty \frac{1}{n^p}$, where $p$ is a positive real number. While the $p$-series converges for values of $p$ greater than 1, it diverges when $p=1$. This divergence, though seemingly counterintuitive, can be understood by examining the behavior of the series and employing key convergence tests.
Unveiling the Divergence: Why $p=1$ Makes the Series Unstable
The $p$-series with $p=1$ is known as the harmonic series, represented as $\sum_{n=1}^\infty \frac{1}{n}$. It might seem that as $n$ gets increasingly large, the terms of the series become vanishingly small, suggesting convergence. However, the harmonic series, despite its seemingly diminishing terms, diverges. This divergence arises from the slow, but persistent, accumulation of the terms.
The Integral Test: A Powerful Tool for Convergence Analysis
One method to demonstrate the divergence of the harmonic series is the integral test. This test compares the series to an improper integral and leverages the relationship between the series' convergence and the integral's finiteness. For the harmonic series, the integral test states:
$\sum_{n=1}^\infty \frac{1}{n} \ge \int_1^\infty \frac{1}{x} dx$
Evaluating the integral, we get:
$\int_1^\infty \frac{1}{x} dx = \lim_{b \to \infty} [\ln(x)]1^b = \lim{b \to \infty} (\ln(b) - \ln(1)) = \lim_{b \to \infty} \ln(b) = \infty$
Since the integral diverges, the integral test tells us that the harmonic series, our $p$-series with $p=1$, also diverges.
The Comparison Test: Unveiling the Hidden Relationship
Another method to understand the divergence is the comparison test. This test compares the series in question with a known divergent series. For the harmonic series, we can compare it to the series $\sum_{n=1}^\infty \frac{1}{2^n}$. This geometric series with a common ratio of $\frac{1}{2}$ is known to diverge.
We observe that for all $n \ge 1$, $\frac{1}{n} \ge \frac{1}{2^n}$. Since the larger series, the harmonic series, is greater than or equal to the divergent geometric series, the comparison test tells us that the harmonic series also diverges.
Understanding the Impact of p = 1
The divergence of the $p$-series when $p=1$ has significant implications. It demonstrates that even though the terms of a series may approach zero, the series may still diverge. The divergence arises from the slow, but steady, accumulation of the terms.
This understanding is crucial in various mathematical fields. For example, in the realm of probability and statistics, the harmonic series serves as a foundation for understanding the behavior of certain random variables. In analysis, it provides insights into the convergence and divergence of other infinite series.
Conclusion: The Harmonic Series - A Divergent Series with Deep Implications
The divergence of the $p$-series when $p = 1$ underscores the subtle interplay between the terms of a series and its convergence. The harmonic series, with its seemingly diminishing terms, exemplifies that even slowly decreasing terms can accumulate to infinity. Understanding this divergence is essential for comprehending the nature of infinite series and its implications across various branches of mathematics.