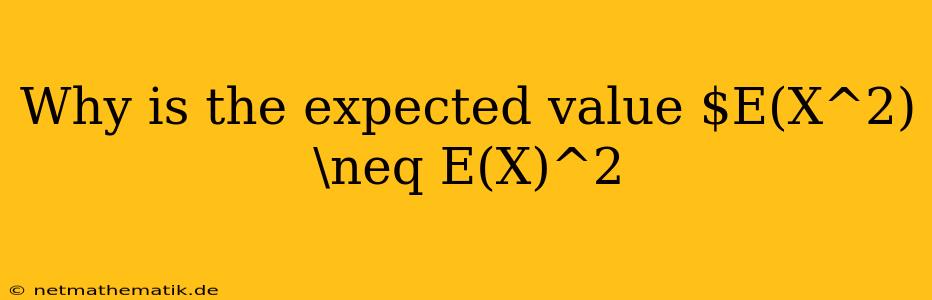In probability and statistics, the concept of expected value plays a crucial role in understanding the average outcome of a random variable. Often, we encounter situations where we need to calculate the expected value of a function of a random variable, such as the square of the variable. A common misconception arises when attempting to calculate the expected value of the square of a random variable, $E(X^2)$. It is tempting to assume that $E(X^2)$ is simply equal to the square of the expected value of the variable, $E(X)^2$. However, this is not generally true. This article delves into the reasons behind this inequality and explores the significance of this distinction.
Understanding Expected Value
Before diving into the core issue, let's briefly review the concept of expected value. For a discrete random variable X with possible values $x_1, x_2, ..., x_n$ and corresponding probabilities $p_1, p_2, ..., p_n$, the expected value, denoted as $E(X)$, is calculated as follows:
$E(X) = \sum_{i=1}^n x_i p_i$
In essence, the expected value represents the weighted average of the possible values of the random variable, where the weights are the probabilities of each value.
Why $E(X^2) \neq E(X)^2$
The fundamental reason why $E(X^2)$ is not necessarily equal to $E(X)^2$ lies in the nature of expectation. The expected value operator, $E(\cdot)$, is linear. This means that for any constants $a$ and $b$ and any random variables $X$ and $Y$, the following properties hold:
- E(aX + bY) = aE(X) + bE(Y) (Linearity)
However, the squaring operation is not a linear operation. The square of the sum of two numbers is not equal to the sum of their squares.
$ (a + b)^2 \neq a^2 + b^2$
To illustrate this with respect to expected value, consider the following:
$E(X^2) = E(X \cdot X)$
Since squaring is not linear, we cannot simply distribute the expectation operator:
$E(X \cdot X) \neq E(X) \cdot E(X) = E(X)^2$
Example: The Case of a Fair Coin Toss
Let's consider a simple example to solidify this understanding. Imagine flipping a fair coin once. Let the random variable X represent the number of heads obtained.
- X = 1 with probability 1/2 (Heads)
- X = 0 with probability 1/2 (Tails)
Therefore, the expected value of X is:
$E(X) = (1 \times \frac{1}{2}) + (0 \times \frac{1}{2}) = \frac{1}{2}$
Now let's calculate $E(X^2)$:
$E(X^2) = (1^2 \times \frac{1}{2}) + (0^2 \times \frac{1}{2}) = \frac{1}{2}$
And finally, $E(X)^2$:
$E(X)^2 = (\frac{1}{2})^2 = \frac{1}{4}$
Clearly, in this example, $E(X^2) \neq E(X)^2$.
Significance of the Distinction
Understanding the distinction between $E(X^2)$ and $E(X)^2$ is crucial in various statistical contexts. It plays a significant role in:
-
Variance and Standard Deviation: The variance of a random variable X, denoted as $Var(X)$, is defined as the expected value of the squared deviation from the mean:
$Var(X) = E[(X - E(X))^2]$
Expanding this expression leads to:
$Var(X) = E(X^2) - [E(X)]^2$
The distinction between $E(X^2)$ and $E(X)^2$ is critical for accurately calculating the variance and subsequently, the standard deviation.
-
Moment Generating Functions: The moment generating function of a random variable is a powerful tool used in probability and statistics. It is defined as:
$M_X(t) = E(e^{tX})$
The moments of the distribution can be obtained by differentiating the moment generating function at t = 0. The $n$th moment is given by:
$E(X^n) = M_X^{(n)}(0)$
Calculating the moments of the distribution requires understanding the difference between $E(X^n)$ and $E(X)^n$.
-
Probability Distributions: The distinction between $E(X^2)$ and $E(X)^2$ is essential in characterizing different probability distributions. For instance, the mean and variance of a normal distribution are completely determined by the expected value and variance, which in turn involve $E(X)$ and $E(X^2)$.
Conclusion
The inequality between $E(X^2)$ and $E(X)^2$ arises because the squaring operation is not linear, while the expectation operator is. This distinction is crucial for correctly calculating variances, standard deviations, moment generating functions, and for understanding various probability distributions. Remember that $E(X^2)$ represents the expected value of the square of the random variable, whereas $E(X)^2$ represents the square of the expected value of the random variable. By understanding this difference, you can avoid common errors and gain a deeper appreciation for the intricacies of probability and statistics.