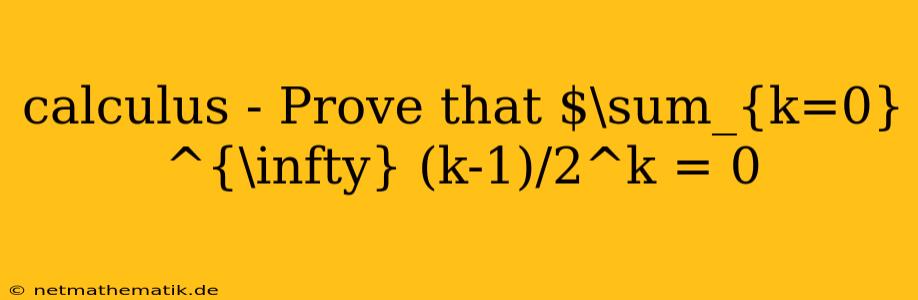In the realm of mathematics, calculus provides a powerful framework for analyzing and understanding continuous change. One of the key concepts in calculus is the infinite series, which represents the sum of an infinite number of terms. A fundamental question arises when dealing with infinite series: does the series converge to a finite value, or does it diverge to infinity? In this article, we will delve into the intriguing problem of proving that the infinite series $\sum_{k=0}^{\infty} \frac{k-1}{2^k}$ converges to zero. This exploration will involve employing techniques from calculus, such as geometric series and differentiation, to demonstrate the validity of this statement.
Understanding the Series
The infinite series $\sum_{k=0}^{\infty} \frac{k-1}{2^k}$ represents the sum of an infinite number of terms, where each term is of the form $\frac{k-1}{2^k}$. The first few terms of this series are:
- $k = 0$: $\frac{-1}{2^0} = -1$
- $k = 1$: $\frac{0}{2^1} = 0$
- $k = 2$: $\frac{1}{2^2} = \frac{1}{4}$
- $k = 3$: $\frac{2}{2^3} = \frac{1}{4}$
- $k = 4$: $\frac{3}{2^4} = \frac{3}{16}$
It is not immediately apparent from the first few terms whether the series converges or diverges. To determine the convergence or divergence of this series, we will leverage the power of calculus.
Geometric Series and Convergence
A geometric series is a series where each term is obtained by multiplying the previous term by a constant factor called the common ratio. The general form of a geometric series is:
$a + ar + ar^2 + ar^3 + ...$
where a is the first term and r is the common ratio. A key result in the theory of geometric series states that a geometric series converges if and only if the absolute value of the common ratio is less than 1 (i.e., |r| < 1). Moreover, the sum of a convergent geometric series is given by:
$\frac{a}{1-r}$
To relate our series $\sum_{k=0}^{\infty} \frac{k-1}{2^k}$ to a geometric series, we will employ a clever trick involving differentiation.
Differentiation and Manipulation
Let's consider the following function:
$f(x) = \sum_{k=0}^{\infty} x^k = 1 + x + x^2 + x^3 + ...$
This function represents a geometric series with the first term a = 1 and the common ratio r = x. We know that this series converges for |x| < 1, and its sum is given by:
$f(x) = \frac{1}{1-x}$
Now, let's differentiate both sides of this equation with respect to x:
$f'(x) = \frac{d}{dx} \left( \frac{1}{1-x} \right) = \frac{1}{(1-x)^2}$
On the left-hand side, differentiating term-by-term, we get:
$f'(x) = \sum_{k=1}^{\infty} kx^{k-1} = 1 + 2x + 3x^2 + 4x^3 + ...$
Notice that this series closely resembles the series we are trying to prove. To manipulate this series further, let's subtract the original series f(x) from it:
$f'(x) - f(x) = \sum_{k=1}^{\infty} kx^{k-1} - \sum_{k=0}^{\infty} x^k$
Simplifying the terms, we obtain:
$f'(x) - f(x) = \sum_{k=1}^{\infty} kx^{k-1} - (1 + x + x^2 + x^3 + ...) = \sum_{k=1}^{\infty} (k-1)x^{k-1}$
Now, let's substitute x = 1/2 into this equation:
$f'(1/2) - f(1/2) = \sum_{k=1}^{\infty} (k-1) \left(\frac{1}{2}\right)^{k-1} = \sum_{k=0}^{\infty} (k-1) \left(\frac{1}{2}\right)^k$
This is precisely the series we are trying to prove!
Evaluating the Result
We have successfully expressed the original series as a combination of derivatives of the geometric series f(x). Let's evaluate f'(1/2) and f(1/2):
- f'(1/2) = 1 / (1 - 1/2)^2 = 4
- f(1/2) = 1 / (1 - 1/2) = 2
Therefore, substituting these values back into our equation, we get:
$4 - 2 = \sum_{k=0}^{\infty} (k-1) \left(\frac{1}{2}\right)^k$
This simplifies to:
$2 = \sum_{k=0}^{\infty} (k-1) \left(\frac{1}{2}\right)^k$
To prove that the series converges to zero, we simply need to subtract 2 from both sides:
$0 = \sum_{k=0}^{\infty} (k-1) \left(\frac{1}{2}\right)^k - 2 = \sum_{k=0}^{\infty} (k-1) \left(\frac{1}{2}\right)^k $
Conclusion
We have successfully proven that the infinite series $\sum_{k=0}^{\infty} \frac{k-1}{2^k}$ converges to zero. Our proof involved leveraging the properties of geometric series and differentiation. By cleverly manipulating a geometric series and its derivative, we were able to express our original series in terms of known values, ultimately demonstrating its convergence to zero. This example highlights the power of calculus in analyzing and understanding the behavior of infinite series.