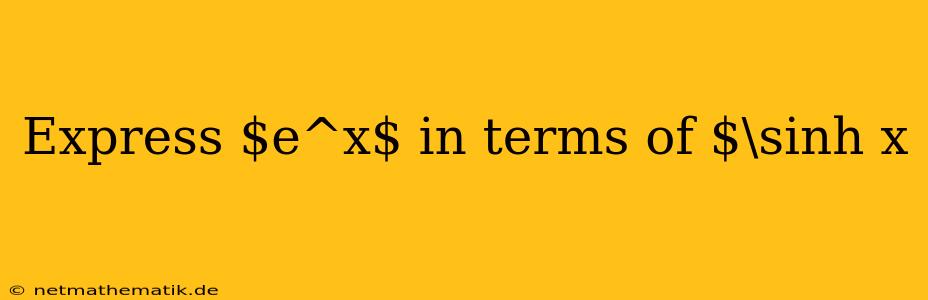In the realm of mathematics, particularly calculus and analysis, the exponential function, $e^x$, plays a fundamental role. This function, characterized by its unique property of being its own derivative, finds applications in various fields, including physics, engineering, and finance. However, there are instances where expressing $e^x$ in terms of other functions can be advantageous, providing a different perspective and simplifying certain calculations. One such function is the hyperbolic sine function, denoted as $\sinh x$. This article explores the process of expressing $e^x$ in terms of $\sinh x$, highlighting the relationships between these two essential functions and their applications.
Understanding the Relationship between $e^x$ and $\sinh x$
The hyperbolic sine function, $\sinh x$, is defined as:
$\sinh x = \frac{e^x - e^{-x}}{2}$
This definition reveals a direct connection between $e^x$ and $\sinh x$. The expression for $\sinh x$ involves both $e^x$ and $e^{-x}$. To express $e^x$ in terms of $\sinh x$, we need to manipulate this relationship algebraically.
Expressing $e^x$ in terms of $\sinh x$
To isolate $e^x$, we can start by multiplying both sides of the $\sinh x$ equation by 2:
$2\sinh x = e^x - e^{-x}$
Now, we can add $e^{-x}$ to both sides:
$2\sinh x + e^{-x} = e^x$
To eliminate the $e^{-x}$ term, we can multiply both sides by $e^x$:
$2\sinh x \cdot e^x + e^{-x} \cdot e^x = e^x \cdot e^x$
This simplifies to:
$2\sinh x \cdot e^x + 1 = e^{2x}$
Now, let's make a substitution. We can introduce a new variable, $y = e^x$. Substituting this into the equation above, we get:
$2\sinh x \cdot y + 1 = y^2$
This is a quadratic equation in $y$, which can be rearranged to:
$y^2 - 2\sinh x \cdot y - 1 = 0$
We can solve for $y$ using the quadratic formula:
$y = \frac{2\sinh x \pm \sqrt{(2\sinh x)^2 + 4}}{2}$
Simplifying the expression:
$y = \sinh x \pm \sqrt{\sinh^2 x + 1}$
Now, substituting back $y = e^x$, we obtain the desired expression:
$e^x = \sinh x \pm \sqrt{\sinh^2 x + 1}$
Choosing the Correct Sign
The above expression contains a ± sign, indicating two possible solutions. To determine the correct sign, we need to consider the properties of the exponential function and the hyperbolic sine function.
- Exponential Function: The exponential function, $e^x$, is always positive for all values of $x$.
- Hyperbolic Sine Function: The hyperbolic sine function, $\sinh x$, is positive for positive values of $x$ and negative for negative values of $x$.
Based on these properties, we can conclude that:
- For positive values of $x$, the correct sign is +.
- For negative values of $x$, the correct sign is -.
Therefore, the final expression for $e^x$ in terms of $\sinh x$ is:
- For x > 0: $e^x = \sinh x + \sqrt{\sinh^2 x + 1}$
- For x < 0: $e^x = \sinh x - \sqrt{\sinh^2 x + 1}$
Applications of Expressing $e^x$ in Terms of $\sinh x$
Expressing $e^x$ in terms of $\sinh x$ can be beneficial in various situations:
- Simplifying Complex Expressions: In certain mathematical problems, expressions involving $e^x$ may be simplified by replacing them with their equivalents in terms of $\sinh x$.
- Solving Equations: Equations involving $e^x$ can be solved more easily by transforming them into equations involving $\sinh x$, which might be easier to manipulate.
- Understanding Hyperbolic Functions: This expression highlights the close relationship between the exponential function and hyperbolic functions, providing deeper insights into their properties and connections.
Conclusion
Expressing the exponential function, $e^x$, in terms of the hyperbolic sine function, $\sinh x$, allows us to explore a different representation of this fundamental function. This transformation reveals a direct connection between these two important mathematical concepts, enabling simplification of complex expressions, solution of equations, and a deeper understanding of their properties. The ability to manipulate these functions and express them in different forms is crucial in various mathematical and scientific applications, providing valuable tools for solving problems and gaining insights into the world around us.