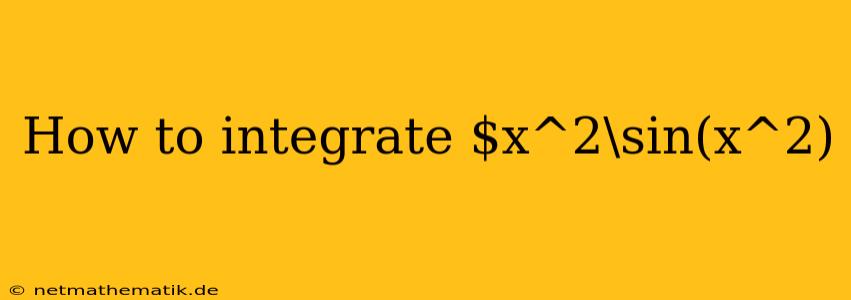Integrating functions can be a challenging task, especially when dealing with complex expressions. One such example is the integral of $x^2\sin(x^2)$. This integral doesn't have a straightforward solution using elementary functions. However, we can employ a technique called integration by parts to tackle this problem. This article will guide you through the process of integrating $x^2\sin(x^2)$, highlighting the steps involved and the key concepts behind this method.
Understanding Integration by Parts
Integration by parts is a powerful technique used to find the integral of a product of two functions. It is derived from the product rule of differentiation. The formula for integration by parts is:
$\int u , dv = uv - \int v , du$
where:
- $u$ and $v$ are differentiable functions of $x$.
- $du$ and $dv$ are the differentials of $u$ and $v$, respectively.
The success of this technique hinges on strategically choosing the functions $u$ and $dv$ so that the integral on the right-hand side is simpler to evaluate than the original integral.
Integrating $x^2\sin(x^2)$
Let's apply integration by parts to find the integral of $x^2\sin(x^2)$.
-
Choosing u and dv:
We start by choosing our functions $u$ and $dv$. Here, we will select:
- $u = x^2$ (Choosing $u$ as a function that simplifies when differentiated)
- $dv = \sin(x^2) , dx$ (Choosing $dv$ as a function that is relatively easy to integrate)
-
Finding du and v:
Now, we need to find the differentials $du$ and the integral $v$:
- $du = 2x , dx$
- $v = \int \sin(x^2) , dx$
The integral of $\sin(x^2)$ doesn't have a closed-form solution in terms of elementary functions. This is where we will encounter a slight complication. We'll address this issue later.
-
Applying the Formula:
Plugging our choices for $u$, $dv$, $du$, and $v$ into the integration by parts formula:
$\int x^2\sin(x^2) , dx = x^2 \int \sin(x^2) , dx - \int (2x) \left( \int \sin(x^2) , dx \right) , dx$
This doesn't look much simpler than our original integral. This is due to the presence of the integral of $\sin(x^2)$ which we cannot evaluate directly.
-
Dealing with the Unsolvable Integral:
Since we cannot find a closed-form expression for $\int \sin(x^2) , dx$, we need a different approach. We can introduce a new integral, often denoted as $I$:
$I = \int x^2\sin(x^2) , dx$
Our integration by parts yielded:
$I = x^2 \int \sin(x^2) , dx - 2 \int x \left( \int \sin(x^2) , dx \right) , dx$
Notice that the term $\int \sin(x^2) , dx$ appears again within the second integral. This suggests that we can use integration by parts again, but this time on the second integral.
-
Second Application of Integration by Parts:
Let's focus on the second integral: $\int x \left( \int \sin(x^2) , dx \right) , dx$. We can apply integration by parts again:
- $u = x$
- $dv = \int \sin(x^2) , dx$
Therefore, $du = dx$ and $v = \int \sin(x^2) , dx$. Applying the integration by parts formula:
$\int x \left( \int \sin(x^2) , dx \right) , dx = x \int \sin(x^2) , dx - \int \left( \int \sin(x^2) , dx \right) , dx$
-
Combining Results:
Substituting this result back into our equation for $I$:
$I = x^2 \int \sin(x^2) , dx - 2 \left[ x \int \sin(x^2) , dx - \int \left( \int \sin(x^2) , dx \right) , dx \right]$
Simplifying:
$I = x^2 \int \sin(x^2) , dx - 2x \int \sin(x^2) , dx + 2 \int \left( \int \sin(x^2) , dx \right) , dx$
Now, we notice that the term $\int \sin(x^2) , dx$ appears multiple times. Let's denote this integral as $S$:
$S = \int \sin(x^2) , dx$
Our equation for $I$ becomes:
$I = x^2S - 2xS + 2 \int S , dx$
We can simplify further:
$I = (x^2 - 2x)S + 2 \int S , dx$
-
Expressing the Integral in Terms of S:
We now have an equation for $I$ in terms of $S$. Remember that $I$ is the integral we want to find, and $S$ is the integral of $\sin(x^2)$ that we cannot evaluate directly.
-
Final Solution:
Unfortunately, we cannot express the integral of $x^2\sin(x^2)$ in terms of elementary functions. We have arrived at an expression that involves the integral of $\sin(x^2)$, which is not a standard integral.
Therefore, the integral of $x^2\sin(x^2)$ is:
$\int x^2\sin(x^2) , dx = (x^2 - 2x) \int \sin(x^2) , dx + 2 \int \left( \int \sin(x^2) , dx \right) , dx + C$
where $C$ is the constant of integration.
Conclusion
The integration of $x^2\sin(x^2)$ demonstrates a key aspect of calculus: not every integral can be expressed in terms of elementary functions. While we cannot find a closed-form solution, the process of applying integration by parts provides us with a valuable result, expressing the integral in terms of the integral of $\sin(x^2)$. This approach underscores the power of integration by parts for tackling complex integrals and highlights the limitations of elementary functions in representing all integrals.