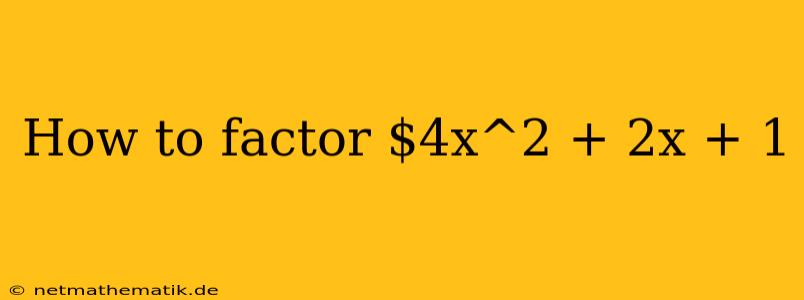Factoring quadratic expressions is a fundamental skill in algebra, and it's often used in solving equations, simplifying expressions, and understanding the behavior of functions. One common type of quadratic expression is the trinomial, which has three terms. In this article, we will explore how to factor the specific trinomial $4x^2 + 2x + 1$ and delve into the general concepts of factoring trinomials.
Understanding the Trinomial
The trinomial $4x^2 + 2x + 1$ is a quadratic expression because the highest power of the variable x is 2. To factor this expression, we aim to rewrite it as a product of two binomials. Let's break down the steps involved:
1. Identify the Coefficients
The first step is to identify the coefficients of each term in the trinomial:
- Coefficient of the squared term (a): 4
- Coefficient of the linear term (b): 2
- Constant term (c): 1
2. Find Two Numbers with Specific Properties
We need to find two numbers that:
- Multiply to give the product of a and c (ac): In our case, this is 4 * 1 = 4
- Add up to the coefficient of the linear term (b): In our case, this is 2.
Let's think of the factors of 4:
- 1 and 4
- 2 and 2
The pair 2 and 2 satisfy both conditions: 2 * 2 = 4 and 2 + 2 = 4.
3. Rewrite the Linear Term
Now, rewrite the middle term (2x) using the two numbers we found:
$4x^2 + 2x + 1 = 4x^2 + 2x + 2x + 1$
4. Factor by Grouping
Group the first two terms and the last two terms:
$(4x^2 + 2x) + (2x + 1)$
Factor out the greatest common factor (GCF) from each group:
$2x(2x + 1) + 1(2x + 1)$
Notice that both terms now have a common factor of $(2x + 1)$:
$(2x + 1)(2x + 1)$
5. Final Result
Therefore, the factored form of the trinomial $4x^2 + 2x + 1$ is $(2x + 1)(2x + 1)$, or simply $(2x + 1)^2$.
Generalizing the Process
The steps we used to factor $4x^2 + 2x + 1$ can be generalized to factor any trinomial of the form $ax^2 + bx + c$, where a, b, and c are constants:
- Identify the coefficients a, b, and c.
- Find two numbers that multiply to ac and add up to b.
- Rewrite the middle term (bx) using these two numbers.
- Factor by grouping.
- Simplify the result to obtain the factored form.
Tips for Factoring Trinomials
Here are a few additional tips that can help you factor trinomials:
- Look for common factors: Before attempting to factor, check if all the terms have a common factor. If so, factor it out first.
- Consider special cases: Be aware of the special cases of factoring, such as perfect square trinomials and difference of squares.
- Practice, practice, practice: Factoring trinomials is a skill that improves with practice. Work through various examples to become more comfortable with the process.
Conclusion
Factoring quadratic trinomials is a valuable skill in algebra. Understanding the process of factoring, and especially the example of factoring $4x^2 + 2x + 1$, provides a solid foundation for manipulating and solving various algebraic expressions and equations. By practicing and applying the steps outlined above, you can master this fundamental skill.