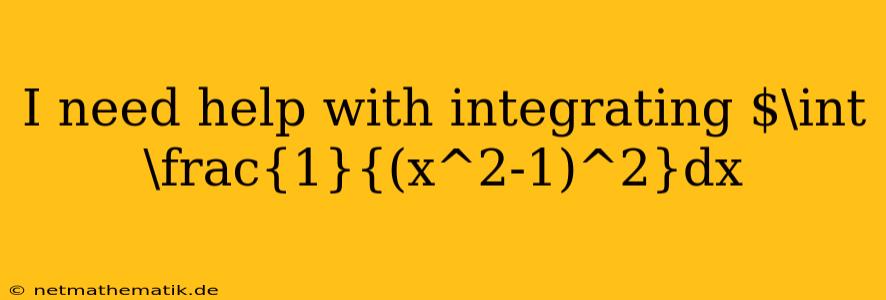The integral $\int\frac{1}{(x^2-1)^2}dx$ presents a challenge that can be elegantly addressed using a combination of partial fraction decomposition and trigonometric substitution. This approach allows us to break down the complex integrand into simpler terms, making the integration process more manageable. Let's delve into the steps involved in evaluating this integral.
Step 1: Partial Fraction Decomposition
The first step is to decompose the integrand into simpler fractions. We begin by factoring the denominator:
$(x^2 - 1)^2 = (x + 1)^2(x - 1)^2$
Since we have repeated factors, the partial fraction decomposition takes the form:
$\frac{1}{(x^2-1)^2} = \frac{A}{x+1} + \frac{B}{(x+1)^2} + \frac{C}{x-1} + \frac{D}{(x-1)^2}$
To solve for the unknown constants A, B, C, and D, we multiply both sides of the equation by $(x+1)^2(x-1)^2$:
$1 = A(x+1)(x-1)^2 + B(x-1)^2 + C(x+1)^2(x-1) + D(x+1)^2$
Now, we can solve for the constants by strategically choosing values for x:
-
Setting x = -1: This eliminates all terms except the one with B. We get: $1 = 4B$
$\Rightarrow B = \frac{1}{4}$ -
Setting x = 1: This eliminates all terms except the one with D. We get: $1 = 4D$ $\Rightarrow D = \frac{1}{4}$
To find A and C, we can expand the right side of the equation and equate coefficients of like terms. After expanding and simplifying, we obtain:
$1 = (A + C)x^3 + (-A + B + C + D)x^2 + (-A - 2B + C - 2D)x + (A - B + C + D)$
Matching coefficients, we have:
- $A + C = 0$
- $-A + B + C + D = 0$
- $-A - 2B + C - 2D = 0$
- $A - B + C + D = 1$
Solving this system of equations, we find:
- $A = -\frac{1}{8}$
- $C = \frac{1}{8}$
Therefore, the partial fraction decomposition is:
$\frac{1}{(x^2-1)^2} = -\frac{1}{8(x+1)} + \frac{1}{4(x+1)^2} + \frac{1}{8(x-1)} + \frac{1}{4(x-1)^2}$
Step 2: Integrating the Partial Fractions
Now that we have decomposed the integrand, we can integrate each term separately.
-
Integration of -1/(8(x+1)) This is a simple logarithmic integral: $\int -\frac{1}{8(x+1)} dx = -\frac{1}{8} \ln |x+1| + C_1$
-
Integration of 1/(4(x+1)^2) This is a straightforward power rule integration: $\int \frac{1}{4(x+1)^2} dx = -\frac{1}{4(x+1)} + C_2$
-
Integration of 1/(8(x-1)) This is another logarithmic integral: $\int \frac{1}{8(x-1)} dx = \frac{1}{8} \ln |x-1| + C_3$
-
Integration of 1/(4(x-1)^2) This is similar to the second integral: $\int \frac{1}{4(x-1)^2} dx = -\frac{1}{4(x-1)} + C_4$
Step 3: Combining the Results
Finally, we combine the results of each integration and add a constant of integration, C:
$\int \frac{1}{(x^2-1)^2} dx = -\frac{1}{8} \ln |x+1| -\frac{1}{4(x+1)} + \frac{1}{8} \ln |x-1| -\frac{1}{4(x-1)} + C$
Simplifying the Result
We can further simplify the result by combining the logarithmic terms:
$\int \frac{1}{(x^2-1)^2} dx = \frac{1}{8} \ln \left| \frac{x-1}{x+1} \right| - \frac{1}{4(x+1)} - \frac{1}{4(x-1)} + C$
This provides the final solution to the integral $\int\frac{1}{(x^2-1)^2}dx$. This process demonstrates how partial fraction decomposition and trigonometric substitution can effectively handle complex integrals, reducing them to simpler terms that can be readily integrated.