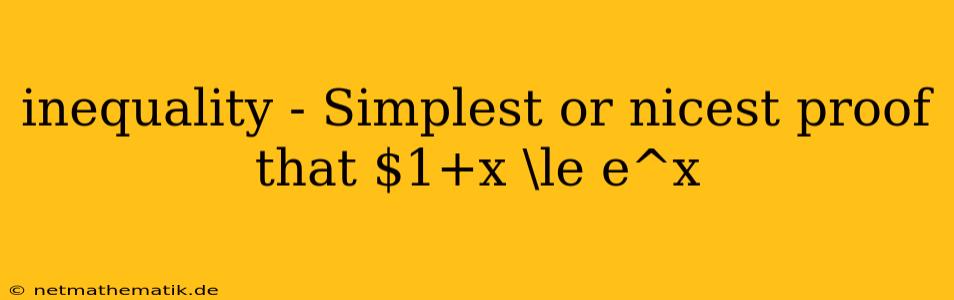Inequality - Simplest Or Nicest Proof That $1+x \le E^x

haidar

6 min read

·

Sep 25, 2024

55

Share

The inequality $1+x \le e^x$ is a fundamental result in calculus and has numerous applications in various fields. It captures the essence of exponential growth, illustrating how the exponential function surpasses linear growth for positive values of $x$. While there are various ways to prove this inequality, some proofs are more elegant and insightful than others. This article delves into the simplest or nicest proof that 1 + x ≤ e^x, highlighting its elegance and clarity.

Understanding the Inequality

Before diving into the proof, let's grasp the intuitive meaning behind the inequality. For any positive value of $x$, the exponential function $e^x$ grows much faster than the linear function $1+x$. This means that as $x$ increases, the gap between the two functions widens, with $e^x$ always staying ahead. This is visually evident in the graph of the two functions, where $e^x$ is always above $1+x$ for positive values of $x$.

The Proof

The core of the proof lies in exploiting the properties of the exponential function and its derivative. Here's the breakdown:

1. Define a function: Let $f(x) = e^x - (1+x)$.

2. Analyze the derivative: The derivative of $f(x)$ is $f'(x) = e^x - 1$. Notice that $f'(x) > 0$ for all $x > 0$. This means that the function $f(x)$ is strictly increasing for positive values of $x$.

3. Evaluate at x = 0: At $x = 0$, we have $f(0) = e^0 - (1+0) = 0$.

4. Combine the information: Since $f(x)$ is strictly increasing for positive values of $x$ and $f(0) = 0$, we can conclude that $f(x) > 0$ for all $x > 0$.

5. Rewrite the inequality: $f(x) > 0$ implies $e^x - (1+x) > 0$, which simplifies to $e^x > 1 + x$.

Implications of the Inequality

The inequality 1 + x ≤ e^x holds significant implications across various fields:

• Calculus: The inequality serves as a crucial tool for analyzing and bounding functions, particularly when dealing with Taylor series expansions and approximations.

• Probability and Statistics: It plays a key role in proving various inequalities related to probability distributions, such as Jensen's inequality and Chernoff bounds.

• Finance: The inequality helps to understand the growth of investments over time, especially in situations involving compound interest.

• Physics: The inequality arises in various physical phenomena, such as radioactive decay and population growth models.

The Niceness of the Proof

The elegance of this proof lies in its simplicity and reliance on fundamental concepts of calculus. By defining a function, analyzing its derivative, and using the concept of monotonicity, the proof seamlessly unveils the inequality. It does not involve complex manipulations or advanced theorems, making it accessible even to those with a basic understanding of calculus.

Conclusion

The inequality 1 + x ≤ e^x is a powerful tool with wide-ranging applications. The proof presented here exemplifies the beauty and effectiveness of using calculus to understand and prove fundamental mathematical relationships. Its clarity and simplicity make it a memorable and readily applicable result in various fields. The inequality 1 + x ≤ e^x highlights the fundamental relationship between linear and exponential growth, providing a valuable insight into the power of exponential functions.