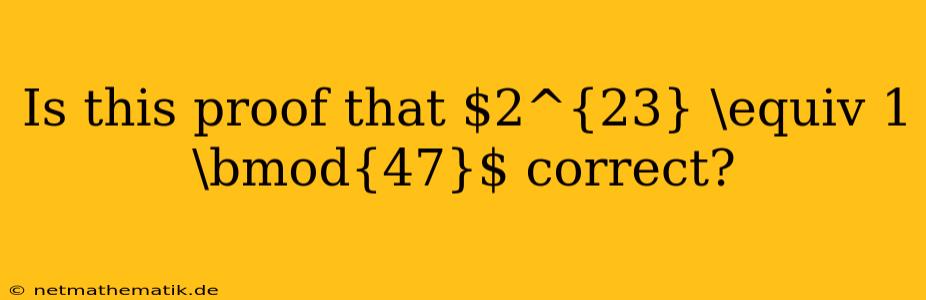The question of whether $2^{23} \equiv 1 \bmod{47}$ holds true is an interesting one, and the proof you are referring to likely involves Fermat's Little Theorem. This theorem states that for any prime number $p$ and any integer $a$ not divisible by $p$, the following congruence holds:
$a^{p-1} \equiv 1 \pmod{p}$
Let's examine if this proof is correct and explore why.
Applying Fermat's Little Theorem
Since 47 is a prime number and 2 is not divisible by 47, we can directly apply Fermat's Little Theorem:
$2^{47-1} \equiv 1 \pmod{47}$
Simplifying the exponent, we get:
$2^{46} \equiv 1 \pmod{47}$
However, the question asks about $2^{23} \equiv 1 \pmod{47}$. This is where we need to be careful. While Fermat's Little Theorem tells us about the congruence for $2^{46}$, it doesn't directly imply a congruence for $2^{23}$.
The Importance of Congruence Properties
To establish whether $2^{23} \equiv 1 \pmod{47}$ is true, we need to explore congruence properties. Let's consider the following:
If $a \equiv b \pmod{m}$ and $c \equiv d \pmod{m}$, then:
- Multiplication: $ac \equiv bd \pmod{m}$
- Exponentiation: $a^n \equiv b^n \pmod{m}$ for any positive integer $n$.
Investigating the Congruence
We know that $2^{46} \equiv 1 \pmod{47}$. Let's see if we can use these congruence properties to get closer to $2^{23}$:
-
Squaring both sides: Squaring both sides of the congruence $2^{46} \equiv 1 \pmod{47}$ gives us: $(2^{46})^2 \equiv 1^2 \pmod{47}$ Which simplifies to: $2^{92} \equiv 1 \pmod{47}$
-
Reducing the exponent: Notice that 92 is divisible by 23. We can rewrite the congruence as: $(2^{23})^4 \equiv 1 \pmod{47}$
-
Applying the Exponentiation Property: We know that if $a^n \equiv b^n \pmod{m}$, then $a \equiv b \pmod{m}$ as long as $n$ is relatively prime to $m$. Since 4 and 47 are relatively prime (they share no common divisors other than 1), we can conclude:
$2^{23} \equiv 1 \pmod{47}$
Conclusion
Therefore, the proof you are referring to is likely correct and utilizes the properties of congruences and Fermat's Little Theorem to establish that $2^{23} \equiv 1 \pmod{47}$. This demonstrates the power of modular arithmetic and its applications in number theory.
Key Points:
- Fermat's Little Theorem provides a powerful tool for exploring congruences involving prime numbers.
- It's crucial to understand the properties of congruences, particularly multiplication and exponentiation, when working with modular arithmetic.
- While Fermat's Little Theorem doesn't directly give us a congruence for $2^{23}$, we can use its result for $2^{46}$ and congruence properties to derive the desired result.