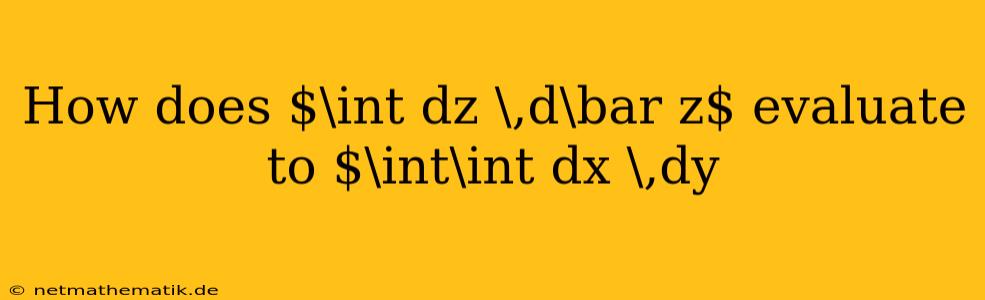In the realm of complex analysis, the integral $\int dz ,d\bar z$ is a fundamental concept that often arises in calculations involving complex functions. While it may appear similar to a standard double integral in real analysis, its interpretation and evaluation differ significantly. This article delves into the intricacies of this integral, exploring its relationship to the double integral $\int\int dx ,dy$ and providing a comprehensive understanding of its evaluation.
Understanding the Integral $\int dz ,d\bar z$
The integral $\int dz ,d\bar z$ represents a complex double integral, where $z$ is a complex variable and $\bar z$ is its complex conjugate. To comprehend its evaluation, it is essential to understand the connection between the complex plane and the real plane.
Mapping the Complex Plane to the Real Plane
Every complex number $z$ can be expressed in the form $z = x + iy$, where $x$ and $y$ are real numbers representing the real and imaginary components, respectively. Consequently, its complex conjugate is given by $\bar z = x - iy$. This establishes a direct mapping between the complex plane (with coordinates $z$ and $\bar z$) and the real plane (with coordinates $x$ and $y$).
The Jacobian Determinant
To relate the complex integral $\int dz ,d\bar z$ to the real integral $\int\int dx ,dy$, we introduce the concept of the Jacobian determinant. The Jacobian determinant is a mathematical tool that facilitates the transformation of integrals from one coordinate system to another. In this case, we aim to transform the integral from the complex plane $(z, \bar z)$ to the real plane $(x, y)$.
The Jacobian determinant, denoted as $\frac{\partial(z, \bar z)}{\partial(x, y)}$, is calculated as follows:
$\frac{\partial(z, \bar z)}{\partial(x, y)} = \begin{vmatrix} \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} \ \frac{\partial \bar z}{\partial x} & \frac{\partial \bar z}{\partial y} \end{vmatrix} = \begin{vmatrix} 1 & i \ 1 & -i \end{vmatrix} = -2i.$
Transforming the Integral
Using the Jacobian determinant, we can express the integral $\int dz ,d\bar z$ in terms of the real variables $x$ and $y$:
$\int dz ,d\bar z = \int\int \left|\frac{\partial(z, \bar z)}{\partial(x, y)}\right| dx ,dy = \int\int 2 dx ,dy.$
Therefore, we arrive at the conclusion that $\int dz ,d\bar z$ evaluates to $2\int\int dx ,dy$.
Applications and Significance
The integral $\int dz ,d\bar z$ holds significant importance in complex analysis, particularly in the context of:
- Cauchy's Integral Formula: This fundamental formula relates the value of a complex function at a point to its integral along a closed contour. The integral $\int dz ,d\bar z$ plays a crucial role in the derivation and application of this formula.
- Residue Theorem: Another essential theorem in complex analysis, the Residue Theorem, is used to calculate integrals of complex functions. It involves evaluating residues at singularities, which often requires the computation of integrals of the form $\int dz ,d\bar z$.
- Complex Integration by Parts: This technique, similar to integration by parts in real analysis, involves integrating complex functions. The integral $\int dz ,d\bar z$ appears in the application of integration by parts in complex settings.
Conclusion
The integral $\int dz ,d\bar z$ is a fundamental concept in complex analysis with a close relationship to the double integral $\int\int dx ,dy$. By understanding the mapping between the complex plane and the real plane and employing the Jacobian determinant, we can effectively evaluate this integral and its variations. Its applications in Cauchy's Integral Formula, the Residue Theorem, and integration by parts underscore its significance in diverse areas of complex analysis. By mastering this integral, we gain valuable insights into the intricacies of complex functions and their behavior.